【题目】阅读下列材料:
如图1,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2外公切线,A、B为切点,
求证:AC⊥BC
证明:过点C作⊙O1和⊙O2的内公切线交AB于D,
∵DA、DC是⊙O1的切线
∴DA=DC.
∴∠DAC=∠DCA.
同理∠DCB=∠DBC.
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证明过程中使用了哪些定理?请写出两个定理的名称或内容;
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图2),已知A、B两点的坐标为(﹣4,0),(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
(3)根据(2)中所确定的抛物线,试判断这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.


参考答案:
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)由切线长相等可知用了切线长定理;由三角形的内角和是180°,可知用了三角形内角和定理;
(2)先根据勾股定理求出![]() 点坐标,再用待定系数法即可求出经过
点坐标,再用待定系数法即可求出经过![]() 三点的抛物线的函数解析式;
三点的抛物线的函数解析式;
(3)过![]() 作两圆的公切线,交
作两圆的公切线,交![]() 于点
于点![]() ,由切线长定理可求出
,由切线长定理可求出![]() 点坐标,根据
点坐标,根据![]() 两点的坐标可求出过
两点的坐标可求出过![]() 两点直线的解析式,根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式,再把抛物线的顶点坐标代入直线的解析式看是否适合即可.
两点直线的解析式,根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式,再把抛物线的顶点坐标代入直线的解析式看是否适合即可.
试题解析:(1)DA、DC是![]() 的切线,
的切线,
∴DA=DC.应用的是切线长定理;
![]() ,应用的是三角形内角和定理.
,应用的是三角形内角和定理.
(2)设C点坐标为(0,y),则![]()
即![]()
即![]() ,解得y=2(舍去)或y=2.
,解得y=2(舍去)或y=2.
故C点坐标为(0,2),
设经过![]() 三点的抛物线的函数解析式为
三点的抛物线的函数解析式为![]()
则 解得
解得
故所求二次函数的解析式为![]()
(3)过C作两圆的公切线CD交AB于D,则AD=BD=CD,由A(4,0),B(1,0)可知![]()
设过CD两点的直线为y=kx+b,则
 解得
解得
故此一次函数的解析式为![]()
∵过![]() 的直线必过C点且与直线
的直线必过C点且与直线![]() 垂直,
垂直,
故过![]() 的直线的解析式为
的直线的解析式为![]()
由(2)中所求抛物线的解析式可知抛物线的顶点坐标为![]()
代入直线解析式得![]() 故这条抛物线的顶点落在两圆的连心
故这条抛物线的顶点落在两圆的连心![]() 上.
上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,
 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段
 ,且使
,且使 ,连接
,连接 ;
;(2)线段
 的长为________,
的长为________, 的长为________,
的长为________,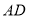 的长为________;
的长为________;(3)
 是________三角形,四边形
是________三角形,四边形 的面积是________;
的面积是________;(4)若点
 为
为 的中点,
的中点, 为
为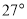 ,则
,则 的度数为________.
的度数为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(观察思考)
怎样判断两条直线是否平行?
如图①,很难看出直线a、n是否平行,可添加“第三条线”(截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.在部分代数问题中,很难用算术直接计算出结果,于是,引入字母解决复杂问题,我们称引入的字母为“辅助元”.事实上,使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题.

(理解运用)
(1)计算
 这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.
这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.(拓展提高)
(2)若关于x,y的方程组
 的解是
的解是 ,则关于x、y的方程组
,则关于x、y的方程组 的解为 .
的解为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图①,当点D在边BC上时,且n等于30°,则∠BAD= ,∠CDE= ;
(2)如图②,当点D运动到点B左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由;
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请在图③中画出图形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y
 =-3x的图象与反比例函数y
=-3x的图象与反比例函数y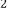 =
= 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12.
的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12. (1)求k的值;
(2)根据图象,当y
 <y
<y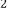 时,写出自变量x的取值范围.
时,写出自变量x的取值范围.
相关试题

