【题目】探究活动:
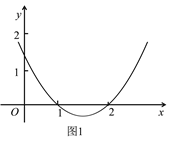
利用函数![]() 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
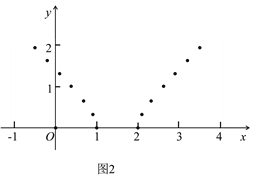
(2)如图2,小东列表描出了函数![]() 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;
(3)解决问题:设方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() ,方程
,方程
![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() .若
.若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接).
参考答案:
【答案】(1)![]() 或
或![]() ;(2)见解析;(3)x1<x3<x4<x2
;(2)见解析;(3)x1<x3<x4<x2
【解析】(1)根据二次根式的性质,列出不等式,解之即可;
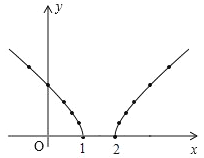
(2)由于x≤1或x≥2,所以函数图象应该是两条分支,根据对称性,补全另一分支即可;
(3)将方程的根转化为两函数图象交点的横坐标,作出函数图象,一目了然.
(1)∵(x-1)(x-2)≥0,
∴x≤1或x≥2;
(2)根据自变量x的取值范围可知,当x≥2时也有对应的函数图象,
补全后的函数图象如图所示:
(3)方程![]() 等价于方程
等价于方程![]() ,
,
方程的两根x1、x2相当于函数y=![]() 与函数
与函数![]() 图象的两个交点的横坐标,
图象的两个交点的横坐标,
方程x2-3x+2=![]() x+b的两根为x3、x4,相当于函数y=x2-3x+2=(x-1)(x-2)与函数y=
x+b的两根为x3、x4,相当于函数y=x2-3x+2=(x-1)(x-2)与函数y=![]() x+b图象的两个交点的横坐标,
x+b图象的两个交点的横坐标,
又∵1<b<![]() ,
,
所以,在同一平面直角从标系中,画出函数图象,如图所示:
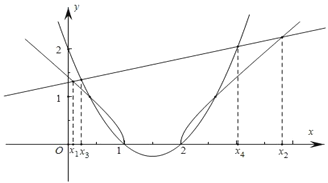
故x1<x3<x4<x2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为
 元.
元.(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为
 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚准备用一段长 44 米的篱笆围成三角形,用于养鸡。已知一条边长 x 米,第二条边是第一条边的 3 倍多 6 米。
(1)若能围成一个等腰三角形,求三边长
(2)若第一边长最短,写出 x 的取值范围 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
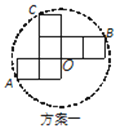
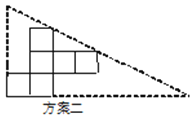
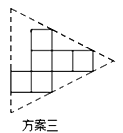
说明:方案一图形中的圆过点A,B,C,圆心O也是正方形的顶点;
回答问题(直接写出结果):
(1)方案二中,直角三角形纸片的两条直角边长分别为_______cm和_______cm;
(2)小明通过计算,发现方案一中纸片的利用率是________(填准确值),近似值约为38.2%.相比之下,方案二的利用率是________%.小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=90°,AB=BC,D在边 AC上,AE⊥BD于 E
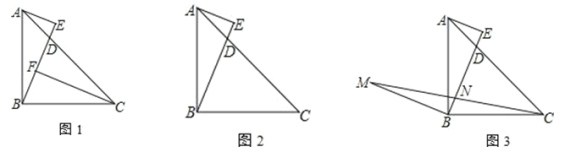
(1)如图1,作 CF⊥BD于F,求证:CF-AE=EF
(2)如图2,若 BC=CD,求
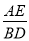 的值
的值(3)如图3,作 BM⊥BE,且 BM=BE,AE=2,EN=4,连 CM交 BE于 N,请直接写出△BCM的面积为___
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
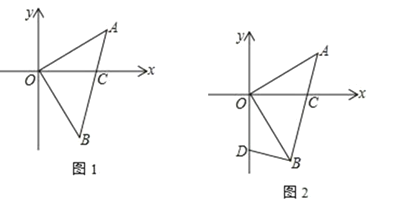
(1) 求△AOB的面积
(2) 如图2,点 D(0,
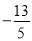 )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB
相关试题

