【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
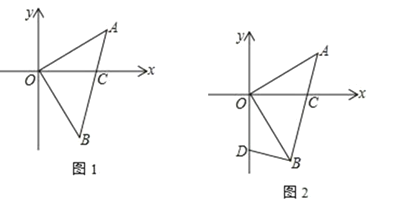
(1) 求△AOB的面积
(2) 如图2,点 D(0,![]() )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据题意可知△ABC为等腰直角三角形,故求出AO的长,即可求出面积;
(2)根据S△AOB=S△AOC+S△BOC,由OC为底,△AOC与△BOC以OC为底的高之和为5,可求出OC的长,得到OD=OC,再证明△AOC≌△BOD,即可证明BD⊥AB
(1)∵∠AOB=90°,OA=OB,
∴△ABC为等腰直角三角形,
∵A(3,2),
∴OA=![]() =OB
=OB
∴S△AOB=![]()
(2)∵S△AOB=S△AOC+S△BOC=![]()
∵△AOC与△BOC以OC为底的高之和为5,
∴S△AOB=![]()
故OC=![]() ,
,
∵D(0,![]() )
)
∴OD=OC,
∵∠AOB=90°,
∴∠AOC+∠BOC=∠BOD+∠BOC,
∴∠AOC=∠BOD
又OA=OB,
∴△AOC≌△BOD,
∴∠DBC=∠DBO+∠OBC=∠CAO+∠OBC=90°,
∴BD⊥AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究活动:
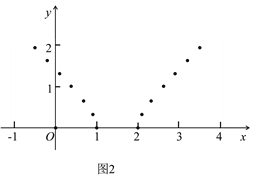
利用函数
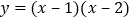 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数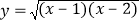 的图象与性质.
的图象与性质.下面是小东的探究过程,请补充完整:
(1)函数
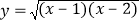 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;(2)如图2,小东列表描出了函数
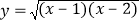 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;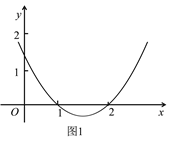
(3)解决问题:设方程
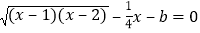 的两根为
的两根为 、
、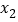 ,且
,且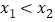 ,方程
,方程 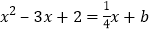 的两根为
的两根为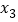 、
、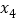 ,且
,且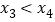 .若
.若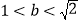 ,则
,则 、
、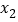 、
、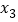 、
、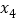 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=90°,AB=BC,D在边 AC上,AE⊥BD于 E
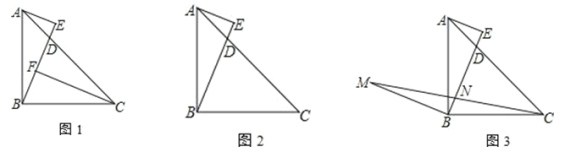
(1)如图1,作 CF⊥BD于F,求证:CF-AE=EF
(2)如图2,若 BC=CD,求
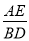 的值
的值(3)如图3,作 BM⊥BE,且 BM=BE,AE=2,EN=4,连 CM交 BE于 N,请直接写出△BCM的面积为___
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
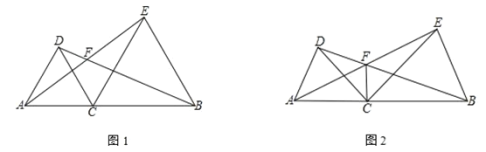
(1)如图 1,若∠ACD=60°,则∠AFD=
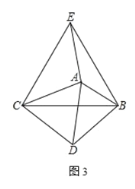
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上
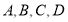 四个点.
四个点. 
(1)按下列要求画图(不写画法)
①连接
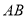 ,
,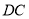 ;②作直线
;②作直线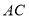 ;③作射线
;③作射线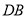 ,交
,交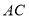 于点
于点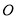 .
. (2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段
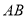 ,
,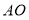 ,
,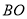 ,可知
,可知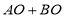 __________
__________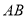 (填“
(填“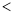 ”,“
”,“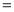 ”或“
”或“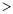 ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB =90°,AC = BC =2,AB =
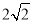 ,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.
,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
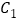 :
: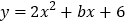 与抛物线
与抛物线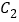 关于y轴对称, 抛物线
关于y轴对称, 抛物线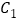 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.(1)求b和m的值;
(2)求抛物线
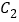 的解析式;
的解析式;(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线
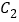 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.
相关试题

