搜索
【题目】如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．
（1）求证：四边形AECD是菱形；
（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．
参考答案：
【答案】（1）证明见解析；（2）直角三角形．
【解析】试题分析：（1）四边形ABCD中，AB∥CD，过C作CE∥AD交AB于E，则四边形AECD是平行四边形（两组对边分别平行的四边形是平行四边形），因为AB∥CD，所以
；AC平分∠BAD，所以
，因此
，所以AD=CD，所以四边形AECD是菱形
（2）由（1）知四边形AECD是菱形，所以AE=CE；点E是AB的中点，AE=BE，所以CE=AE=BE，所以△ABC是直角三角形（斜边上的中线等于斜边的一半是直角三角形）
-
科目： 来源： 题型：
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：
由于a≠0，方程ax2+bx+c=0变形为：
x2+
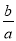x=﹣
，…第一步x2+
x+（
）2=﹣
+（
）2，…第二步（x+
）2=
，…第三步x+
=
（b2﹣4ac＞0），…第四步x=
，…第五步嘉淇的解法从第 步开始出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是 ．
用配方法解方程：x2﹣2x﹣24=0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的高，DE∥AC，DF∥AB，则△ABC满足条件________时，四边形AEDF是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．
（1）求证：四边形EFCD是菱形；
（2）如果AB=8，求D、F两点间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．
（1）求证：四边形ADCE是菱形；
（2）求证：BC=ED．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设I是△ABC的内心，O是△ABC的外心，∠A=80°，则∠BIC=________，∠BOC=________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P为⊙O外一点，PA、PB为⊙O的切线，A、B为切点，弦AB与PO交于C，⊙O半径为1，PO=2，则PA_______，PB=________，PC=_______AC=______，BC=______∠AOB=________．
相关试题
