搜索
【题目】如图，AD是△ABC的高，DE∥AC，DF∥AB，则△ABC满足条件________时，四边形AEDF是菱形．
参考答案：
【答案】AB=AC或∠B=∠C
【解析】∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形.
所以当四边形AEDF中有一组邻边相等时，它就是菱形了.
由此在△ABC中可添加条件：（1）AB=AC或（2）∠B=∠C.
（1）当添加条件“AB=AC”时，
∵AD是△ABC的高，AB=AC，
∴点D是BC边的中点，
又∵DE∥AC，DF∥AB，
∴点E、F分别是AB、AC的中点，
∴AE=
AB，AF=
AC，
∴AE=AF，
∴平行四边形AEDF是菱形.
（2）当添加条件“∠B=∠C”时，
则由∠B=∠C可得AB=AC，同（1）的方法可证得：AE=AF，
∴平行四边形AEDF是菱形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】南校区本学期对初三学生体育选考项目---引体向上（仅男生项目）进行抽样调查，已知完成15个可以拿到100分，完成23个为最高120分，A表示学生做引体向上23个或以上，B表示做15-22个，C表示做10-14个，D表示做9个或9个以下.根据调查结果绘制了不完整的统计图.
成绩
频数（人数）
频率
A
28
x
B
14
0.2
C
m
0.3
D
n
y
（1）抽样学生数为 人，x= ，y= ；
（2）补全条形统计图；
（3）若南校区初三共有720名学生，男女比例为7:5，请估计一共有多少学生可以拿到100分及以上？
-
科目： 来源： 题型：
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：
由于a≠0，方程ax2+bx+c=0变形为：
x2+
x=﹣
，…第一步x2+
x+（
）2=﹣
+（
）2，…第二步（x+
）2=
，…第三步x+
=
（b2﹣4ac＞0），…第四步x=
，…第五步嘉淇的解法从第 步开始出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是 ．
用配方法解方程：x2﹣2x﹣24=0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：
由于a≠0，方程ax2+bx+c=0变形为：
x2+
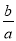x=﹣
，…第一步x2+
x+（
）2=﹣
+（
）2，…第二步（x+
）2=
，…第三步x+
=
（b2﹣4ac＞0），…第四步x=
，…第五步嘉淇的解法从第 步开始出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是 ．
用配方法解方程：x2﹣2x﹣24=0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．
（1）求证：四边形EFCD是菱形；
（2）如果AB=8，求D、F两点间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．
（1）求证：四边形AECD是菱形；
（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．
（1）求证：四边形ADCE是菱形；
（2）求证：BC=ED．
相关试题
