【题目】如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少 . 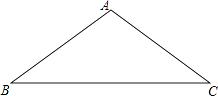
参考答案:
【答案】![]()
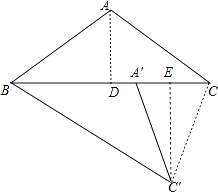
【解析】解:作AD⊥BC于D,C′E⊥BC于E,如图1,
∵AB=AC,
∴BD=CD= ![]() BC=4,
BC=4,
在Rt△ABD中,AD= ![]() =4,
=4,
∴S△ABC= ![]() ×3×8=12,
×3×8=12,
∵△ABC绕着点B旋转的△A′BC′,
∴A′B=A′C′=AB=5,△A′BC′≌△ABC,
∴A′C=3,S△A′BC′=12,
而S△A′BC′= ![]() 5C′E,
5C′E,
∴ ![]() 5C′E=12,解得C′E=
5C′E=12,解得C′E= ![]() ,
,
在Rt△A′C′E中,A′E= ![]() =
= ![]() ,
,
∴CE=3﹣ ![]() =
= ![]() ,
,
在Rt△C′CE中,CC′= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】根据题目的已知条件,利用旋转的性质的相关知识可以得到问题的答案,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根. 其中正确的结论是( )

A.③④
B.②④
C.②③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价30元。厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:一套西装送一条领带; 方案二:西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(x>20)。
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);若该客户按方案②购买,需付款 元(用含x的代数式表示)°
(2)若x=30,两种方案中,通过计算说明选择按哪种方案购买较为合算。
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的方案,并计算出所需的钱数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=
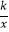 (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).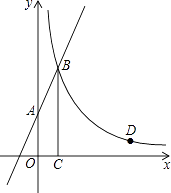
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=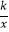 (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知α是锐角,且sin(α﹣15°)=
 计算:
计算:  ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+(  )﹣1的值.
)﹣1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,坐标原点O到一次函数y=kx-2k+1图像的距离的最大值为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示数a,b,A、B两点之间的距离表示为
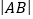 。数轴上A、B两点之间的距离
。数轴上A、B两点之间的距离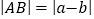 。
。回答下列问题:
(1)数轴上表示-1和-4的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A之和B之间的距离是 ,如果
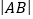 =2,那么x的值是 ;
=2,那么x的值是 ; (3) 若x表示一个有理数,且﹣1<x<3,则|x﹣3|+|x+1|= ;
(4)若x表示一个有理数,且|x﹣1|+|x+2|>3,则有理数x的取值范围是 .
相关试题

