搜索
【题目】在平面直角坐标系中，坐标原点O到一次函数y=kx-2k+1图像的距离的最大值为___．
参考答案：
【答案】
【解析】
一次函数y=kx-2k+1的图像过定点（2，1），原点O（0，0）到过（2，1）所有直线的距离h小于等于（0，0）到（2，1）的距离，O（0，0）到（2，1）的距离为 .
解：∵y=kx-2k+1=（x-2）k+1,当x=2时，无论k为何值，y=1，
∴直线y=kx-2k+1的图像过定点A（2，1），
又∵点到直线的距离等于点到直线的垂线段的长，
∴原点O（0，0）到过A（2，1）所有直线的距离h小于等于（0，0）到（2，1）的距离，
∴O（0，0）到（2，1）的距离为
=，即坐标原点O到一次函数y=kx-2k+1图像的距离的最大值为，此时OA与直线垂直，点A是垂足.
故答案为：.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=2x+3与y轴交于A点，与反比例函数y=
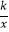（x＞0）的图象交于点B，过点B作BC⊥x轴于点C，且C点的坐标为（1，0）．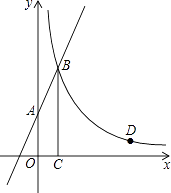
（1）求反比例函数的解析式；
（2）点D（a，1）是反比例函数y=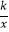 （x＞0）图象上的点，在x轴上是否存在点P，使得PB+PD最小？若存在，求出点P的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC=5，BC=8，将△ABC绕着点B旋转的△A′BC′，点A的对应点A′，点C的对应点C′．如果点A′在BC边上，那么点C和点C′之间的距离等于多少 ．
-
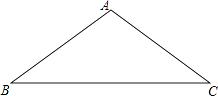
科目： 来源： 题型：
查看答案和解析>>【题目】已知α是锐角，且sin（α﹣15°）=
计算： 
﹣4cosα﹣（π﹣3.14）0+tanα+（ 
）﹣1的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】点A、B在数轴上分别表示数a，b，A、B两点之间的距离表示为
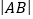。数轴上A、B两点之间的距离
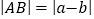。回答下列问题：
(1)数轴上表示－1和－4的两点之间的距离是 ；
(2)数轴上表示x和－1的两点A之和B之间的距离是 ，如果
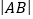＝2，那么x的值是 ； (3) 若x表示一个有理数，且﹣1＜x＜3，则|x﹣3|+|x+1|= ；
(4)若x表示一个有理数，且|x﹣1|+|x+2|＞3，则有理数x的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某次考试中，某班级的数学成绩统计图如图.下列说法错误的是( )
A. 得分在70～80分之间的人数最多 B. 该班的总人数为40
C. 得分在90～100分之间的人数最少 D. 及格(≥60分)人数是26
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB交CD于O，OE⊥AB．
（1）若∠EOD=20°，求∠AOC的度数；
（2）若∠AOC：∠BOC=1：2，求∠EOD的度数．
相关试题
