【题目】已知α是锐角,且sin(α﹣15°)= ![]() 计算:
计算: ![]() ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+( ![]() )﹣1的值.
)﹣1的值.
参考答案:
【答案】解:∵sin(α﹣15°)= ![]() ,
,
∴α﹣15°=30°,
则α=45°,
![]() ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+( ![]() )﹣1
)﹣1
=2 ![]() ﹣4×
﹣4× ![]() ﹣1+1+3
﹣1+1+3
=3.
【解析】首先利用特殊角的三角函数值得出α的度数,再利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值分别化简得出答案.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价30元。厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:一套西装送一条领带; 方案二:西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(x>20)。
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);若该客户按方案②购买,需付款 元(用含x的代数式表示)°
(2)若x=30,两种方案中,通过计算说明选择按哪种方案购买较为合算。
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的方案,并计算出所需的钱数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=
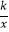 (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).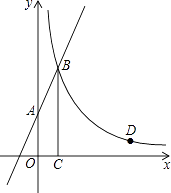
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=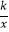 (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少 .
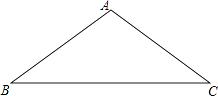
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,坐标原点O到一次函数y=kx-2k+1图像的距离的最大值为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示数a,b,A、B两点之间的距离表示为
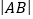 。数轴上A、B两点之间的距离
。数轴上A、B两点之间的距离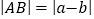 。
。回答下列问题:
(1)数轴上表示-1和-4的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A之和B之间的距离是 ,如果
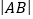 =2,那么x的值是 ;
=2,那么x的值是 ; (3) 若x表示一个有理数,且﹣1<x<3,则|x﹣3|+|x+1|= ;
(4)若x表示一个有理数,且|x﹣1|+|x+2|>3,则有理数x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
相关试题

