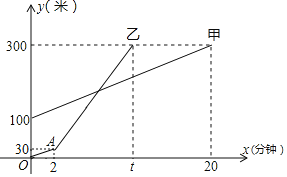
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
参考答案:
【答案】(1)10,120;(2)①![]() ,②能够实现.理由见解析;(3)当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
,②能够实现.理由见解析;(3)当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
【解析】
(1)由时间,速度,路程的基本关系式可解;
(2)①分段代入相关点的坐标,利用待定系数法来求解即可;
②分别计算甲乙距离地面的高度再比较即可;
(3)求出甲的函数解析式,分0≤x≤2时,2<x≤11时,11<x≤20时来讨论即可求解.
(1)甲登山的速度为:(300﹣100)÷20=10米/分,100+10×2=120米,
故答案为:10,120.
(2)①V乙=3V甲=30米/分,
t=2+(300﹣30)÷30=11(分钟),
设2到11分钟,乙的函数解析式为y=kx+b,
∵直线经过A(2,30),(11,300),
∴![]() 解得
解得![]()
∴当2<x≤11时,y=30x﹣30
设当0≤x≤2时,乙的函数关系式为y=ax,
∵直线经过A(2,30)
∴30=2a解得a=15,
∴当0≤x≤2时,y=15x,
综上,![]()
②能够实现.理由如下:
提速5分钟后,乙距地面高度为30×7﹣30=180米.
此时,甲距地面高度为7×10+100=170米.180米>170米,所以此时,乙已经超过甲.
(3)设甲的函数解析式为:y=mx+100,将(20,300)代入得:300=20m+100
∴m=10,
∴y=10x+100.
∴当0≤x≤2时,由(10x+100)﹣15x=80,解得x=4>2矛盾,故此时没有符合题意的解;
当2<x≤11时,由|(10x+100)﹣(30x﹣30)|=80得
|130﹣20x|=80
∴x=2.5或x=10.5;
当11<x≤20时,由300﹣(10x+100)=80得x=12
∴x=2.5或10.5或12.
∴当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求多项式4x2﹣3﹣6x与多项式﹣x2+2x+5的2倍的和.
(2)先化简,再求值:
 ,其中
,其中
(3)已知两个多项式A,B,其中B=﹣2x2+5x﹣3,求A﹣B.小马虎同学在计算时,误将A﹣B错看成了A+B,求得的结果为3x2﹣2x+10.请你帮助这位同学求出正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
……
月销量(件)
200
180
160
140
……
(1)已知该运动服的进价为每件60元,设售价为x元;
请用含有x的式子表示:
①销售该运动服每件的利润是 元;
②月销售量是 件;(直接写结果)
(2)设销售该运动服的月利润为y元,那么售价为多少元时,当月的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A.B对应的数分别为﹣2和7,点M为数轴上一动点.
(1)请画出数轴,并在数轴上标出点A、点B;
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是(A,B)的好点.
①若点M运动到原点O时,此时点M (A,B)的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是(B,A)的好点时,求点M的运动方向和运动时间
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
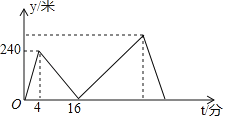
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长
-
科目: 来源: 题型:
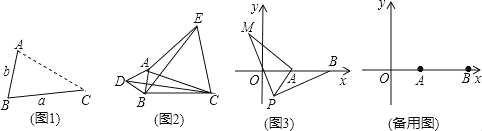
查看答案和解析>>【题目】(1)发现:
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
相关试题

