【题目】如图,![]() 为直线
为直线![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() .
.
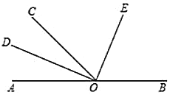
(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)猜想:![]() 是否平分
是否平分![]() ?请直接写出你猜想的结论;
?请直接写出你猜想的结论;
(3)与![]() 互余的角有:______.
互余的角有:______.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)平分;(3)
;(2)平分;(3)![]() 、
、![]() .
.
【解析】
(1)根据角平分线和直角的性质,即可得出∠COE,然后根据平角的性质即可得出∠BOE;
(2)根据角平分线的性质得出![]() ,然后根据余角的性质得出∠COE=∠BOE,即可得出
,然后根据余角的性质得出∠COE=∠BOE,即可得出![]() 平分
平分![]() ;
;
(3)根据余角的性质,即可判定.
(1)∵![]() 平分
平分![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() ,
,
![]() ;
;
(2)平分
∵![]() 平分
平分![]() ,
,
∴![]()
∵![]()
∴∠DOC+∠COE=∠AOD+∠BOE=90°
∴∠COE=∠BOE
∴![]() 平分
平分![]() ;
;
(3)由题意,得∠DOE=∠DOC+∠COE=90°
∠AOD+∠BOE=90°,∠AOD=∠DOC
∴与![]() 互余的角有:
互余的角有:![]() 、
、![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
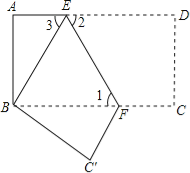
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形
 中,
中, 是对角线
是对角线 上的一点,点
上的一点,点 在
在 的延长线上,且
的延长线上,且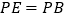
 求证:
求证:
 求证:
求证:
 把正方形
把正方形 改为菱形,其他条件不变(如图
改为菱形,其他条件不变(如图 ②),且
②),且 ,求
,求 的大小.
的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数
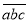 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的  为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

注:水费按月结算,不足1立方米的不收费.若某户居民1月份用水8立方米,则应交水费:2×6+4×(8-6)=20(元).
(1)若该户居民2月份交水费16元,计算该户居民2月份的用水量;
(2)若该户居民3月份用水12.5立方米,则应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=
 x2﹣
x2﹣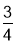 x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
相关试题

