【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
参考答案:
【答案】(1)0;(2)0.
【解析】试题分析:(1)由三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,根据“最优组合”的定义即可求解;
(2)由三位“善雅数”的定义,可得a为偶数,且2+x+y是3的倍数,且2+x+y<30,又由m的各位数字之和为一个完全平方数,可得2+x+y=32=9,继而求得答案.
试题解析:(1)证明:∵三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,∴重新排序后:其中两个数位上数字的和是一个数位上的数字的2倍,∴a+c﹣2b=0,即(a﹣b)﹣(b﹣c)=0,∴F(t)=0;
∵(2)∵m=200+10x+y是“善雅数”,∴x为偶数,且2+x+y是3的倍数,∵x<10,y<10,∴2+x+y<30,∵m的各位数字之和为一个完全平方数,∴2+x+y=32=9,∴当x=0时,y=7,当x=2时,y=5,当x=4时,y=3,当x=6时,y=1,∴所有符合条件的“善雅数”有:207,225,243,261,∴所有符合条件的“善雅数”中F(m)的最大值是=|2﹣3|﹣|3﹣4|=0.
-
科目: 来源: 题型:
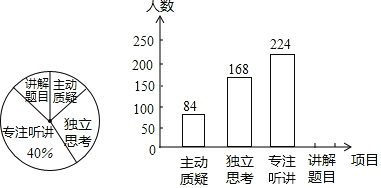
查看答案和解析>>【题目】某市数学调研小组对老师在讲评试卷中学生参与的深度与广度进行评价调查,其评价项目为“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”四项,该调研小组随机抽取了若干名初中七年级学生的参与情况,绘制成如图所示的频数分布直方图和扇形統计图(均不完整),请根据图中所给信息答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将频数分布直方图补充完整;
(3)如果全市有4000名七年级学生,那么在试卷评讲课中,“独立思考”的七年级学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.

(1)若AB=3,AD=
 ,求△BMC的面积;
,求△BMC的面积;(2)点E为AD的中点时,求证:AD=
 BN .
BN . -
科目: 来源: 题型:
查看答案和解析>>【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线
 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
(1)求S△ABD的值;
(2)如图2,若点P是直线AD下方抛物线上一动点,过点P作PF∥y轴交直线AD于点F,作PG∥AC交直线AD于点G,当△PGF的周长最大时,在线段DE上取一点Q,当PQ+
 QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+  QE的值;
QE的值;(3)如图3,M是BC的中点,以CM为斜边作直角△CMN,使CN∥x轴,MN∥y轴,将△CMN沿射线CB平移,记平移后的三角形为△C′M′N′,当点N′落在x轴上即停止运动,将此时的△C′M′N′绕点C′逆时针旋转(旋转度数不超过180°),旋转过程中直线M′N′与直线CA交于点S,与y轴交于点T,与x轴交于点W,请问△CST是否能为等腰三角形?若能,请求出所有符合条件的WN′的长度;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以已知线段
 为弦作⊙
为弦作⊙ ,使其经过已知点
,使其经过已知点 .
.(
 )利用直尺和圆规作圆(保留作图痕迹,不必写出作法).
)利用直尺和圆规作圆(保留作图痕迹,不必写出作法).(
 )若
)若 ,
,  ,求过
,求过 、
、 、
、 三点的圆的半径.
三点的圆的半径.
相关试题

