【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
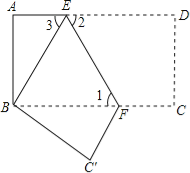
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
参考答案:
【答案】(1)60°,60°;(2)3![]()
【解析】试题分析:(1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=1,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.
解:(1)∵AD∥BC,
∴∠2=∠1=60°;
又∵∠4=∠2=60°,
∴∠3=180°﹣60°﹣60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°﹣60°=30°;
∴BE=2AE=2,
∴AB=![]() =;
=;
∴AD=AE+DE=AE+BE=1+2=3,
∴长方形纸片ABCD的面积S为:ABAD=×3=3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:
计算:(-5)÷
 ×20.
×20.解:原式=(-5)÷
 ×20 (第一步)
×20 (第一步)=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解题过程中有两处错误:
第一处是第________步,错误的原因是__________________________;
第二处是第________步,错误的原因是_______________________.
(2)把正确的解题过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解简单的高次方程:
(1)

(2)
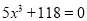
(3)
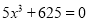
(4)
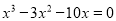
(5)
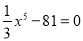
(6)
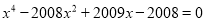
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 中,
中, 分别是
分别是 的中点,连接
的中点,连接 ,则
,则 的周长为( )
的周长为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形
 中,
中, 是对角线
是对角线 上的一点,点
上的一点,点 在
在 的延长线上,且
的延长线上,且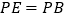
 求证:
求证:
 求证:
求证:
 把正方形
把正方形 改为菱形,其他条件不变(如图
改为菱形,其他条件不变(如图 ②),且
②),且 ,求
,求 的大小.
的大小.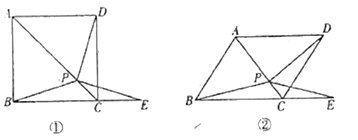
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数
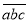 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的  为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
-
科目: 来源: 题型:
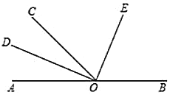
查看答案和解析>>【题目】如图,
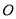 为直线
为直线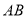 上一点,
上一点,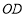 平分
平分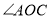 ,
,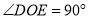 .
.
(1)若
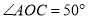 ,求
,求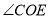 和
和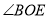 的度数;
的度数;(2)猜想:
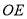 是否平分
是否平分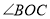 ?请直接写出你猜想的结论;
?请直接写出你猜想的结论;(3)与
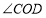 互余的角有:______.
互余的角有:______.
相关试题

