【题目】如图,在长方形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 厘米/秒的速度移动;点
厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 厘米/秒的速度移动,如果
厘米/秒的速度移动,如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间,那么:
(秒)表示移动的时间,那么:

(1)如图1,当![]() 为何值时,线段
为何值时,线段![]() 的长度等于线段
的长度等于线段![]() 的长度?
的长度?
(2)如图2,当![]() 为何值时,
为何值时,![]() 与
与![]() 的长度之和是长方形
的长度之和是长方形![]() 周长的
周长的![]() ?
?
(3)如图3,点![]() 到达点
到达点![]() 后继续以相同速度沿
后继续以相同速度沿![]() 边运动,到达点
边运动,到达点![]() 后停止运动;点
后停止运动;点![]() 到达点
到达点![]() 后继续以相同速度沿
后继续以相同速度沿![]() 边运动,当点
边运动,当点![]() 停止运动时点
停止运动时点![]() 也停止运动.当点
也停止运动.当点![]() 在
在![]() 边上运动时,
边上运动时,![]() 为何值可使线段
为何值可使线段![]() 的长度等于线段
的长度等于线段![]() 长度的一半?
长度的一半?
参考答案:
【答案】(1)当![]() 为
为![]() 时,线段
时,线段![]() 的长度等于线段
的长度等于线段![]() 的长度;(2)当
的长度;(2)当![]() 为2时,
为2时,![]() 与
与![]() 的长度之和是长方形
的长度之和是长方形![]() 周长的
周长的![]() ;(3)
;(3)![]() 为5可使线段
为5可使线段![]() 的长度等于线段
的长度等于线段![]() 长度的一半.
长度的一半.
【解析】
(1)由已知可得2t=4-t;(2)由已知可得t+8-2t=![]() ;(3)由已知可得t-4=
;(3)由已知可得t-4=![]() ,解方程可得.
,解方程可得.
解:(1)由已知可得
2t=4-t
解得t=![]()
(2)由已知可得
t+8-2t=![]()
解得t=2
(3)由已知可得t-4=![]()
解得:t=5
答:(1)当![]() 为
为![]() 时,线段
时,线段![]() 的长度等于线段
的长度等于线段![]() 的长度;(2)当
的长度;(2)当![]() 为2时,
为2时,![]() 与
与![]() 的长度之和是长方形
的长度之和是长方形![]() 周长的
周长的![]() ;(3)
;(3)![]() 为5可使线段
为5可使线段![]() 的长度等于线段
的长度等于线段![]() 长度的一半.
长度的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次献爱心捐款活动中,学校团支部为了解本校学生的各类捐款人数的情况,进行了一次统计调查,并绘制成了统计图①和②,请解答下列问题.
(1)本次共调查了多少名学生.
(2)补全条形统计图.
(3)这些学生捐款数的众数为 ,中位数为 .
(4)求平均每个学生捐款多少元.
(5)若该校有600名学生,那么共捐款多少元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
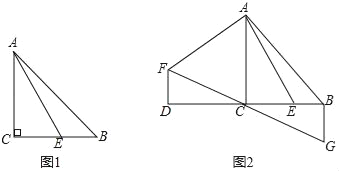
(1)如图1,当∠BAE=15°,CE=
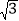 时,求AB的长.
时,求AB的长.(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,德强学校初中部中考屡创佳绩,捷报频传.为了吸纳更多的优质生源,学校决定要新建一栋
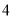 层的教学大楼,每层楼有
层的教学大楼,每层楼有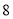 间教室,进出这栋大楼共有
间教室,进出这栋大楼共有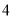 道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对
道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对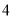 道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,
道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,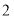 分钟可以通过
分钟可以通过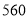 名学生;当同时开启一道正门和一道侧门时
名学生;当同时开启一道正门和一道侧门时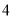 分钟可以通过
分钟可以通过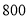 名学生.
名学生.(1)正常情况下,平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低
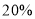 ,安全检查规定,在紧急情况下全大楼的学生应在
,安全检查规定,在紧急情况下全大楼的学生应在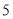 分钟内通过这
分钟内通过这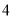 道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这
道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这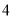 道门是否符合安全规定?请说明理由.
道门是否符合安全规定?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张长方形纸片,
 长为
长为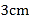 ,
,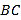 长为
长为 .
. 
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕
 边所在直线旋转一周,则形成的几何体的体积是____
边所在直线旋转一周,则形成的几何体的体积是____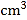 (结果保留
(结果保留 );
);(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留
 ).
).
相关试题

