【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
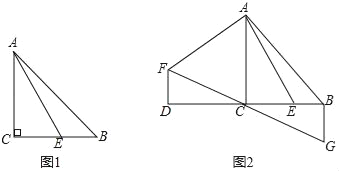
(1)如图1,当∠BAE=15°,CE=![]() 时,求AB的长.
时,求AB的长.
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
参考答案:
【答案】(1)3![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)、根据题意得出△ABC为等腰直角三角形,根据题意得出∠CAE=30°,从而求出AE的长度,然后根据Rt△ACE的性质求出BC的长度,从而得出AB的长度;(2)、连接AD,线段AE绕点A顺时针旋转90°得线段AF,根据旋转的性质得出△ADF和△ABE全等,从而证明△BCG和△DCF全等,从而得出答案.
详解:(1)∵∠ACB=90°,AC=BC,∴△ABC是等腰直角三角形,∴∠BAC=45°,∠BAE=15°,
∴∠CAE=30°,∵CE=![]() ,∴Rt△ACE中,AE=2CE=2
,∴Rt△ACE中,AE=2CE=2![]() ,
,
∴由勾股定理可得,AC=![]() =3, ∴BC=3,
=3, ∴BC=3,
∴Rt△ABC中,由勾股定理可得,AB=![]() =3
=3![]() ;
;
(2)如图所示,连接AD,
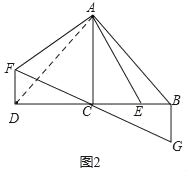
线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°, ∵AC⊥BD,DC=BC,
∴AD=AB,∠ABE=∠ADC=45°,又∵DF⊥DC,∴∠ADF=45°=∠ABE,
∵∠AFD+∠AED=180°=∠AEB+∠AED, ∴∠AFD=∠AEB, ∴△ADF≌△ABE,
∴DF=BE, ∵BG⊥BC,∴∠CBG=∠CDF=90°, 又∵BC=DC,∠BCG=∠DCF,
∴△BCG≌△DCF,∴DF=BG, ∴BG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=
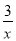 的图象上,求过点A的反比例函数的解析式.
的图象上,求过点A的反比例函数的解析式.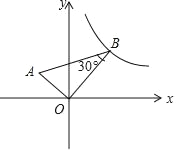
-
科目: 来源: 题型:
查看答案和解析>>【题目】篝火晚会前夕,德强学校附近一超市从厂家购进了甲、乙两种发光道具,甲种道具的每件进价比乙种道具的每件进价少
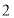 元.若购进甲种道具
元.若购进甲种道具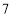 件,乙种道具
件,乙种道具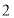 件,需要
件,需要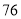 元.
元.(1)求甲、乙两种道具的每件进价分别是多少元?
(2)若该超市从厂家购进了甲乙两种道具共
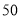 件,所用资金恰好为
件,所用资金恰好为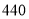 元.在销售时,甲种
元.在销售时,甲种道具的每件售价为
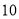 元,要使得这
元,要使得这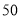 件道具所获利润率为
件道具所获利润率为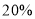 ,乙道具的每件售价为多少元?
,乙道具的每件售价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次献爱心捐款活动中,学校团支部为了解本校学生的各类捐款人数的情况,进行了一次统计调查,并绘制成了统计图①和②,请解答下列问题.
(1)本次共调查了多少名学生.
(2)补全条形统计图.
(3)这些学生捐款数的众数为 ,中位数为 .
(4)求平均每个学生捐款多少元.
(5)若该校有600名学生,那么共捐款多少元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, 厘米,
厘米, 厘米,点
厘米,点 沿
沿 边从点
边从点 开始向点
开始向点 以
以 厘米/秒的速度移动;点
厘米/秒的速度移动;点 沿
沿 边从点
边从点 开始向点
开始向点 以
以 厘米/秒的速度移动,如果
厘米/秒的速度移动,如果 、
、 同时出发,用
同时出发,用 (秒)表示移动的时间,那么:
(秒)表示移动的时间,那么:
(1)如图1,当
 为何值时,线段
为何值时,线段 的长度等于线段
的长度等于线段 的长度?
的长度?(2)如图2,当
 为何值时,
为何值时, 与
与 的长度之和是长方形
的长度之和是长方形 周长的
周长的 ?
?(3)如图3,点
 到达点
到达点 后继续以相同速度沿
后继续以相同速度沿 边运动,到达点
边运动,到达点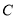 后停止运动;点
后停止运动;点 到达点
到达点 后继续以相同速度沿
后继续以相同速度沿 边运动,当点
边运动,当点 停止运动时点
停止运动时点 也停止运动.当点
也停止运动.当点 在
在 边上运动时,
边上运动时, 为何值可使线段
为何值可使线段 的长度等于线段
的长度等于线段 长度的一半?
长度的一半? -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,德强学校初中部中考屡创佳绩,捷报频传.为了吸纳更多的优质生源,学校决定要新建一栋
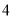 层的教学大楼,每层楼有
层的教学大楼,每层楼有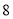 间教室,进出这栋大楼共有
间教室,进出这栋大楼共有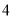 道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对
道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对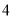 道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,
道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,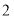 分钟可以通过
分钟可以通过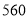 名学生;当同时开启一道正门和一道侧门时
名学生;当同时开启一道正门和一道侧门时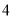 分钟可以通过
分钟可以通过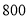 名学生.
名学生.(1)正常情况下,平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低
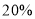 ,安全检查规定,在紧急情况下全大楼的学生应在
,安全检查规定,在紧急情况下全大楼的学生应在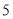 分钟内通过这
分钟内通过这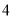 道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这
道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这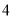 道门是否符合安全规定?请说明理由.
道门是否符合安全规定?请说明理由.
相关试题

