【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
参考答案:
【答案】(1)裁剪出的侧面个数为6x+4(19-x)=(2x+76)个
裁剪出的底面个数为5(19-x)=(-5x+95)个
(2)最多可以做的盒子个数为30个
【解析】
试题(1)因为x张用A方法,则有(38-x)张用B方法,就可以根据题意分别表示出侧面和底面的个数.(2)由题意可得,侧面个数和底面个数之比为3:2,可以列出一元一次方程,求出x的值,从而可得侧面的总数,即可求得.
试题解析:(1)根据题意可得,侧面:![]() (个),底面:
(个),底面:![]() (个).
(个).
(2)根据题意可得,![]() ,解得x=7,所以盒子=
,解得x=7,所以盒子=![]() (个).
(个).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以
 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;②m是方程m2 -12=0的解;③m满足不等式组
 ,④m是12的算术平方根.
,④m是12的算术平方根.A. ①② B. ①③ C. ③ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图: ①分别以A,C为圆心,大于
 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若x,y都是实数,且
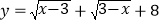 ,求5x+13y+6的立方根;
,求5x+13y+6的立方根;(2)已知△ABC的三边长分别为a,b,c,且满足
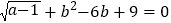 ,求c的取值范围。
,求c的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如
 不能表示为两个互质的整数的商,所以
不能表示为两个互质的整数的商,所以 几个号无理数.可以这样证明:
几个号无理数.可以这样证明:设
 ,a与b是互质的两个整数,且b≠0,则2=
,a与b是互质的两个整数,且b≠0,则2= ,所以a=2b.
,所以a=2b.因为b是整数且不为0,所以a是不为0的偶数.设a=2n(n是整数),
所以b=2n,所以b也是偶数,与a与b是互质的整数矛盾,
所以
 是无理数.
是无理数.仔细阅读上文,然后请证明:
 是无理数。
是无理数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.

相关试题

