【题目】数轴上两点之间的距离等于相对应的两数差的绝对值.
(1)数轴上表示2和5的两点之间的距离是___________;数轴上表示﹣2和﹣8的两点之间的距离是___________;
(2)数轴上表示数x和﹣1的两点之间的距离是2,那么x为_____________;
(3)若某动点表示的数为x,当式子|x+1|+|x﹣2|取得最小值时,相应的x的范围是________.
(4)若某动点表示的数为x,已知数轴上两点![]() 对应的数分别为
对应的数分别为![]() 、3,点
、3,点![]() 为点A点B之间的一点(不与A,B重合),点
为点A点B之间的一点(不与A,B重合),点![]() 对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
![]()
参考答案:
【答案】(1)3;(2)-3或者1;(3)在-1和2之间,包括-1和2;(4)15
【解析】
(1)计算2和5,﹣2和﹣8的差值的绝对值,即可得出答案;
(2)计算-1+2,-1-2,即可得到x的值;
(3)结合数轴和两点间的距离进行分析;
(4)结合数轴和两点间的距离进行分析;
(1)2和5的两点之间的距离为5-2=3,﹣2和﹣8的两点之间的距离为-2-(-8)=6;
(2)-1+2=1,-1-2=-3,
∴x=-3或1;
(3)|x+1|+|x﹣2|的几何意义是:数轴上表示数x的点到表示-1、2两点的距离之和,显然在-1和2之间,包括-1和2时,距离之和最小.
故答案为在-1和2之间,包括-1和2;
(4)|x﹣p|+|x﹣3|+|x﹣p﹣15|的几何意义是:数轴上表示数x的点到表示p、3、p+15三点的距离之和,
∵点![]() 为点A点B之间的一点(不与A,B重合),
为点A点B之间的一点(不与A,B重合),
∴p<3<p+15,
p到p+15的距离为15,显然当x=3时,|x﹣p|+|x﹣3|+|x﹣p﹣15|的最小值为15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中, E、F、G、H分别是边AB、BC、CD、DA的中点,若AC=BD,且EG2+FH2=16,则AC的长为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列
行
第1列
第2列
第3列
第4列
第1行
1
2
3
4
第2行
8
7
6
5
第3行
9
10
11
12
第4行
16
15
14
13
…
…
…
…
…
第n行
…
…
…
…
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
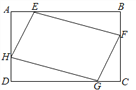
A. 7 B. 10 C. 14 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A、B、C、D四个等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:

(1)抽取了__名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是__;
(4)若A、B、C三个等级为合格,该校初二年级有900名学生,估计全年级生物合格的学生人数.
相关试题

