【题目】如图,在四边形ABCD中, E、F、G、H分别是边AB、BC、CD、DA的中点,若AC=BD,且EG2+FH2=16,则AC的长为________.

参考答案:
【答案】4
【解析】分析:根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形,根据菱形的性质得到EG⊥HF,再由勾股定理得出EH的长,从而得到答案.
详解:如图,设EG和FH相交于点O.
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,根据三角形的中位线的性质知,EH=FG=![]() BD,EF=HG=
BD,EF=HG=![]() AC.
AC.
又∵AC=BD,∴EH=FG=EF=HG,∴四边形EFGH是菱形,∴EG⊥HF,EO=![]() EG,OH=
EG,OH=![]() HF,∴EF=EH=
HF,∴EF=EH=![]() =
=![]() =
=![]() =
=![]() =2,∴AC=2EF=4.
=2,∴AC=2EF=4.

故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3,
 ),B(9,5
),B(9,5  ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,  ,
,  (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(1)求AB所在直线的函数表达式.
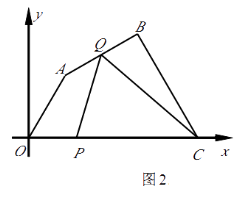
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某粮库已存有粮食100吨,本周内粮库进出粮食的纪录如下(运进记为正,运出记为负):

(1)通过计算,说明本周内哪天粮库剩下的粮食最多?
(2)若运进的粮食为购进的,购买的价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列
行
第1列
第2列
第3列
第4列
第1行
1
2
3
4
第2行
8
7
6
5
第3行
9
10
11
12
第4行
16
15
14
13
…
…
…
…
…
第n行
…
…
…
…
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上两点之间的距离等于相对应的两数差的绝对值.
(1)数轴上表示2和5的两点之间的距离是___________;数轴上表示﹣2和﹣8的两点之间的距离是___________;
(2)数轴上表示数x和﹣1的两点之间的距离是2,那么x为_____________;
(3)若某动点表示的数为x,当式子|x+1|+|x﹣2|取得最小值时,相应的x的范围是________.
(4)若某动点表示的数为x,已知数轴上两点
 对应的数分别为
对应的数分别为 、3,点
、3,点 为点A点B之间的一点(不与A,B重合),点
为点A点B之间的一点(不与A,B重合),点 对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
相关试题

