【题目】(本题满分10分)某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A、B、C、D四个等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:

(1)抽取了__名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是__;
(4)若A、B、C三个等级为合格,该校初二年级有900名学生,估计全年级生物合格的学生人数.
参考答案:
【答案】 (1)50 (2)如图D等级5名(3)72° (4)810
【解析】(1)根据题意得:23÷46%=50(名),
则抽取了50名学生成绩;
故答案为:50;
(2)D等级的学生有50(10+23+12)=5(名),
补全直方图,如图所示:
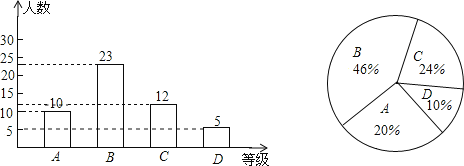
(3)根据题意得:20%×360=72,
故答案为:72;
(4)根据题意得:900×90%=810(人),
则全年级生物合格的学生共约810人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上两点之间的距离等于相对应的两数差的绝对值.
(1)数轴上表示2和5的两点之间的距离是___________;数轴上表示﹣2和﹣8的两点之间的距离是___________;
(2)数轴上表示数x和﹣1的两点之间的距离是2,那么x为_____________;
(3)若某动点表示的数为x,当式子|x+1|+|x﹣2|取得最小值时,相应的x的范围是________.
(4)若某动点表示的数为x,已知数轴上两点
 对应的数分别为
对应的数分别为 、3,点
、3,点 为点A点B之间的一点(不与A,B重合),点
为点A点B之间的一点(不与A,B重合),点 对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
对应的数为p。则式子|x﹣p|+|x﹣3|+|x﹣P﹣15|的最小值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
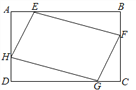
A. 7 B. 10 C. 14 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复

 下表是活动中的一组统计数据:
下表是活动中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
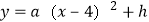 ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a=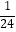 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为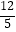 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
相关试题

