【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
参考答案:
【答案】
(1)
解:把A(﹣4,0),B(0,4)代入y=ax2+2xa+c得 ![]() ,解得
,解得 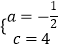 ,
,
所以抛物线解析式为y=﹣ ![]() x2﹣x+4;
x2﹣x+4;
(2)
解:如图1,
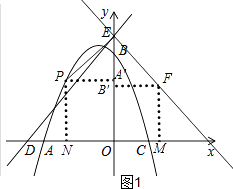
分别过P、F向y轴作垂线,垂足分别为A′、B′,过P作PN⊥x轴,垂足为N,
由直线DE的解析式为:y=x+5,则E(0,5),
∴OE=5,
∵∠PEO+∠OEF=90°,∠PEO+∠EPA′=90°,
∴∠EPA′=∠OEF,
∵PE=EF,∠EA′P=∠EB′F=90°,
∴△PEA′≌△EFB′,
∴PA′=EB′=﹣t,
则d=FM=OB′=OE﹣EB′=5﹣(﹣t)=5+;
(3)
解:如图2,
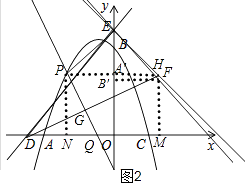
由直线DE的解析式为:y=x+5,
∵EH⊥ED,
∴直线EH的解析式为:y=﹣x+5,
∴FB′=A′E=5﹣(﹣ ![]() t2﹣t+4)=
t2﹣t+4)= ![]() t2+t+1,
t2+t+1,
∴F( ![]() t2+t+1,5+t),
t2+t+1,5+t),
∴点H的横坐标为: ![]() t2+t+1,
t2+t+1,
y=﹣ ![]() t2﹣t﹣1+5=﹣
t2﹣t﹣1+5=﹣ ![]() t2﹣t+4,
t2﹣t+4,
∴H( ![]() t2+t+1,﹣
t2+t+1,﹣ ![]() t2﹣t+4),
t2﹣t+4),
∵G是DH的中点,
∴G( ![]() ,
, ![]() ),
),
∴G( ![]() t2+
t2+ ![]() t﹣2,﹣
t﹣2,﹣ ![]() t2﹣
t2﹣ ![]() t+2),
t+2),
∴PH∥x轴,
∵DG=GH,
∴PG=GQ,
∴ ![]() =
= ![]() t2+
t2+ ![]() t﹣2,
t﹣2,
t= ![]()
![]() ,
,
∵P在第二象限,
∴t<0,
∴t=﹣ ![]() ,
,
∴F(4﹣ ![]() ,5﹣
,5﹣ ![]() ).
).
【解析】本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,考查了直角三角形全等的性质和判定;本题的关键是根据直角三角形全等对应边相等列式得出d与t的函数关系式;同时要注意:若A、B两点的坐标分别为(x1、y1)、(x2、y2),则线段AB中点的坐标为( ![]() ,
, ![]() ).(1)利用待定系数法求二次函数的解析式;(2)如图1,作辅助线构建两个直角三角形,利用斜边PE=EF和两角相等证两直角三角形全等,得PA′=EB′,则d=FM=OE﹣EB′代入列式可得结论,但要注意PA′=﹣t;(3)如图2,根据直线EH的解析式表示出点F的坐标和H的坐标,发现点P和点H的纵坐标相等,则PH与x轴平行,根据平行线截线段成比例定理可得G也是PQ的中点,由此表示出点G的坐标并列式,求出t的值并取舍,计算出点F的坐标.
).(1)利用待定系数法求二次函数的解析式;(2)如图1,作辅助线构建两个直角三角形,利用斜边PE=EF和两角相等证两直角三角形全等,得PA′=EB′,则d=FM=OE﹣EB′代入列式可得结论,但要注意PA′=﹣t;(3)如图2,根据直线EH的解析式表示出点F的坐标和H的坐标,发现点P和点H的纵坐标相等,则PH与x轴平行,根据平行线截线段成比例定理可得G也是PQ的中点,由此表示出点G的坐标并列式,求出t的值并取舍,计算出点F的坐标.
【考点精析】掌握确定一次函数的表达式是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对九(1)班学生进行百米测验,已知女生达标成绩为18秒,下面两图分别是甲、乙两小组各5名女生的成绩统计图.请你根据下面统计图回答问题.
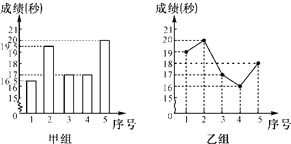
(1)甲、乙两组的达标率分别是多少?
(2)根据图中信息你认为哪个组的成绩相对稳定?
(3)如果老师表扬甲组的成绩好于乙组,那么老师是从各组的平均数、中位数、达标率、方差中的哪个数来说明的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2.
(1)用尺规作图作出镜面BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系;
(3)你是如何思考的?

-
科目: 来源: 题型:
查看答案和解析>>【题目】情系灾区.5月12日我国四川汶川县发生里氏8.0级大地震,地震给四川,甘肃,陕西等地造成巨大人员伤亡和财产损失.灾难发生后,我校师生和全国人民一道,迅速伸出支援的双手,为灾区人民捐款捐物.为了支援灾区学校灾后重建,我校决定象灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套,一辆乙货车可装床架10个和课桌凳10套.
(1)学校如何安排甲、乙两种货车可一次性把这些物资运到灾区?有几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费最少?最少运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+
 =(1+
=(1+ )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:设a+b
 =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn .
.∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
 =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,用含m、n的式子分别表示a、b,得:a= ,b= ;(2)利用探索的结论,找一组正整数a、b、m、n (a、b都不超过20)
填空: +
 =( +
=( +  )2;
)2;(3)若a+6
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值?
)2,且a、m、n均为正整数,求a的值? -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程限期完成,甲队单独做正好按期完成,乙队单独做则要延期3天完成.现两队先合作2天,再由乙队单独做,也正好按期完成.如果设规定的期限为x天,那么根据题意可列出方程:
 =1;
=1;  2
2 =1;③
=1;③ =1;④
=1;④ .其中正确的个数为( )
.其中正确的个数为( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 =0;
=0;(2)
 -1.
-1.
相关试题

