【题目】如图1,一张△ABC纸片,点M、N分别是AC、BC上两点.(均只需写出结论即可)
(1)若沿直线MN折叠,使C点落在BN上,则∠AMC′与∠ACB的数量关系是 .
(2)若折成图2的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(3)若折成图3的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(4)将上述问题推广,如图4,将四边形ABCD纸片沿MN折叠,使点C、D落在四边形ABNM的内部时,∠AMD′+∠BNC′与∠C、∠D之间的数量关系是 .

参考答案:
【答案】(1) ∠AMC′=2∠ACB;(2)∠AMC′+∠BNC′=2∠ACB;(3)∠AMC′-∠BNC′=2∠ACB; (4)∠AMD′+∠BNC′=2(∠C+∠D-180°).
【解析】试题分析:(1)根据折叠性质和三角形的外角定理得出结论;
(2)先根据折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,由两个平角∠CMA和∠CNB得:∠AMC′+∠′BNC′等于360°与四个折叠角的差,化简为结果;
(3)利用两次外角定理得出结论;
(4)与(2)类似,先由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,再由两平角的和为360°得:∠AMD′+∠BNC′=360°﹣2∠DMN﹣2∠CNM,根据四边形的内角和得:∠DMN+∠CNM=360°﹣∠C﹣∠D,代入前式可得结论.
试题解析:解:(1)由折叠得:∠ACB=∠MC′C,∵∠AMC′=∠ACB+∠MC′C,∴∠AMC′=2∠ACB;
故答案为:∠AMC′=2∠ACB;
(2)猜想:∠AMC′+∠BNC′=2∠ACB,理由是:
由折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,∵∠CMA+∠CNB=360°,∴∠AMC′+∠′BNC′=360°﹣∠CMN﹣∠C′MN﹣∠CNM﹣∠C′NM=360°﹣2∠CMN﹣2∠CNM,∴∠AMC′+∠BNC′=2(180°﹣∠CMN﹣∠CNM)=2∠ACB;
(3)∵∠AMC′=∠MDC+∠C,∠MDC=∠C′+∠BNC′,∴∠AMC′=∠C′+∠BNC′+∠C,∵∠C=∠C′,∴∠AMC′=2∠C+∠BNC′,∴∠AMC′﹣∠BNC′=2∠ACB;
(4)由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,∵∠DMA+∠CNB=360°,∴∠AMD′+∠BNC′=360°﹣2∠DMN﹣2∠CNM,∵∠DMN+∠CNM=360°﹣∠C﹣∠D,∴∠AMD′+∠BNC′=360°﹣2(360°﹣∠C﹣∠D)=2(∠C+∠D-180°),故答案为:∠AMD′+∠BNC′=2(∠C+∠D﹣180°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为﹣1,那么与A点相距3个单位长度的点所对应的有理数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=
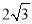 ,则∠EDC的度数为( )
,则∠EDC的度数为( )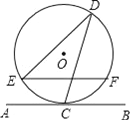
A. 60° B. 90° C. 30° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】法国埃菲尔铁塔的塔身是由许多三角形构成的,设计师运用的几何原理是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的重心是三角形的三条 _________的交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1 400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需__________元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
(3)李大爷现在资金25 000元,他准备再向银行贷不超过25 000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35 000元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数
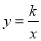 (k≠0)在第一象限的图象经过顶点
(k≠0)在第一象限的图象经过顶点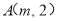 和CD边上的点
和CD边上的点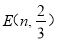 ,过点
,过点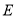 的直线
的直线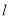 交
交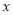 轴于点
轴于点 ,交y轴于点G(0,﹣2),则点
,交y轴于点G(0,﹣2),则点 的坐标是__.
的坐标是__.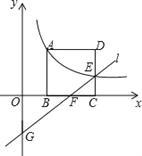
相关试题

