【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )
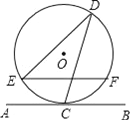
A. 60° B. 90° C. 30° D. 75°
参考答案:
【答案】C
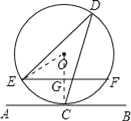
【解析】试题分析:连接OC,与EF交于点G,再连接OE,由AB为圆O的切线,利用切线的性质得到OC与AB垂直,再由EF与AB平行,得到OC与EF垂直,利用垂径定理得到G为EF中点,求出EG的长,在直角三角形OEG中,利用勾股定理求出OG的长,利用直角三角形中一直角边等于斜边的一半,这条直角边所对的角为30°,求出∠OEG度数,进而得到∠EOC度数,利用圆周角定理即可求出所求角度数.如图:连接OC,与EF交于点G,再连接OE,∵AB为圆O的切线,∴OC⊥AB,∵EF∥AB,∴OC⊥EF,∴EG=FG=![]() EF=
EF=![]() ,在Rt△OEG中,OE=2,EG=
,在Rt△OEG中,OE=2,EG=![]() ,根据勾股定理得:OG=1,∴∠OEG=30°,∴∠EOG=60°,∵∠EDC与∠EOC都对弧EC,则∠EDC=30°.故选C.
,根据勾股定理得:OG=1,∴∠OEG=30°,∴∠EOG=60°,∵∠EDC与∠EOC都对弧EC,则∠EDC=30°.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x3x2=2x6
B.x4x2=x8
C.(﹣x2)3=﹣x6
D.(x3)2=﹣x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)某地政府急灾民之所需,立即组织12辆汽车,将A、B、C三种救灾物资共92吨一次性运往灾区,甲、乙、丙三种车型的汽车分别运载A、B、C三种物资,每辆车按运载量满装物资。假设装运A、B品种物资的车辆数分别为
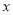 、
、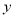 ,根据下表提供的信息解答下列问题:
,根据下表提供的信息解答下列问题:车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
(1)装运C品种物资车辆数为 辆(用含
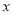 与
与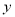 的代数式表示);
的代数式表示);(2)试求A、B、C三种物资各几吨。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为﹣1,那么与A点相距3个单位长度的点所对应的有理数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】法国埃菲尔铁塔的塔身是由许多三角形构成的,设计师运用的几何原理是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一张△ABC纸片,点M、N分别是AC、BC上两点.(均只需写出结论即可)
(1)若沿直线MN折叠,使C点落在BN上,则∠AMC′与∠ACB的数量关系是 .
(2)若折成图2的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(3)若折成图3的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(4)将上述问题推广,如图4,将四边形ABCD纸片沿MN折叠,使点C、D落在四边形ABNM的内部时,∠AMD′+∠BNC′与∠C、∠D之间的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的重心是三角形的三条 _________的交点.
相关试题

