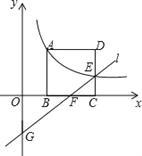
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数![]() (k≠0)在第一象限的图象经过顶点
(k≠0)在第一象限的图象经过顶点![]() 和CD边上的点
和CD边上的点![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,交y轴于点G(0,﹣2),则点
,交y轴于点G(0,﹣2),则点![]() 的坐标是__.
的坐标是__.
参考答案:
【答案】(2.25,0)
【解析】由点A(m,2)得到正方形的边长为2,则BC=2,所以n=2+m,根据反比例图象上的坐标特征得到k=2m=![]() (2+m),解得m=1,则E点坐标为(3,
(2+m),解得m=1,则E点坐标为(3, ![]() ),然后利用待定系数法确定直线GF的解析式为y=
),然后利用待定系数法确定直线GF的解析式为y=![]() ,再求y=0时对应自变量的值,从而得到点F的坐标.
,再求y=0时对应自变量的值,从而得到点F的坐标.
解;方形的顶点A(m,2),
∴正方形的边长为2,
∴BC=2,而点E(n, ![]() ),
),
∴n=2+m,即E点坐标为(2+m, ![]() ),
),
∴k=2m=![]() (2+m),解得m=1,
(2+m),解得m=1,
∴E点坐标为(3, ![]() ),
),
设直线GF的解析式为y=ax+b,
把E(3, ![]() ),G(0,-2)代入得
),G(0,-2)代入得 ,解得
,解得
∴直线GF的解析式为y=![]() ,
,
当y=0时, ![]() =0,
=0,
解得x=2.25,
∴点F的坐标为(2.25,0).
“点睛”此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法确定函数解析式,熟练掌握待定系数法是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一张△ABC纸片,点M、N分别是AC、BC上两点.(均只需写出结论即可)
(1)若沿直线MN折叠,使C点落在BN上,则∠AMC′与∠ACB的数量关系是 .
(2)若折成图2的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(3)若折成图3的形状,猜想∠AMC′、∠BNC′和∠ACB的数量关系是 .
(4)将上述问题推广,如图4,将四边形ABCD纸片沿MN折叠,使点C、D落在四边形ABNM的内部时,∠AMD′+∠BNC′与∠C、∠D之间的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的重心是三角形的三条 _________的交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1 400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需__________元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
(3)李大爷现在资金25 000元,他准备再向银行贷不超过25 000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35 000元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】判定一个三角形是不是等腰三角形,我们经常利用以下的判定方法:“如果一个三角形有两个角相等,那么这两个角所对的边也相等”,请你利用以上判定方法解决下列问题
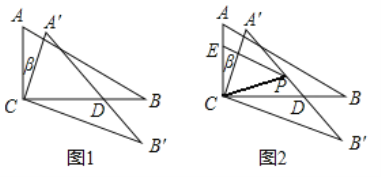
如图1,在△ABC中,∠ACB=90°,∠B=30°,将△ABC绕顶点C顺时针旋转,旋转角为β
(0°<β<180°),得到△A′B′C
(1)设A′B′与CB相交于点D,
①当旋转角为β=25°,∠B′DB= °;
②当AB∥CB′ 时,求证:D是A′B′ 的中点;
(2)如图2,E是AC边上的点,且
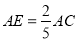 ,P是A′B′边上的点,且∠A′PC=60°,连接EP、CP,已知AC=10,①当β= °时,EP长度最大,最大值为 ;
,P是A′B′边上的点,且∠A′PC=60°,连接EP、CP,已知AC=10,①当β= °时,EP长度最大,最大值为 ;②当β= °时,△ECP的面积最大,最大值为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在0、1、2、3中,哪个数是方程3x﹣2=4x﹣3的解( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的面积之比为1∶4,则它们的周长之比为( )
A.1∶2B.1∶4C.1∶5D.1∶16
相关试题

