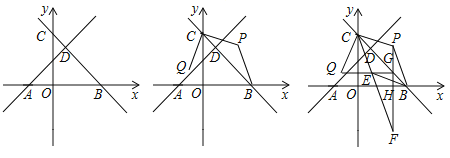
【题目】如图,在平面直角坐标系中,![]() 为坐标原点.直线
为坐标原点.直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,垂足为
,垂足为![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,且点
,且点![]() 坐标为
坐标为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为直线
为直线![]() 右侧第一象限内一点,连接
右侧第一象限内一点,连接![]() 、
、![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段![]() ,点
,点![]() 落在点
落在点![]() 处,设点
处,设点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)在(2)的条件下,过点![]() 作
作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)y=x+2;;(2)Q(-![]() m2+m,4-m);(3)P(
m2+m,4-m);(3)P(![]() ,
,![]() ).
).
【解析】
(1)由已知可得∠DAO=45°,进而得到AD直线的k=1,将点A(-2,0)代入即可;
(2)过点P作x轴、y轴垂线,相交于点M,过点Q作y轴垂线,交于点N,由已知条件可证明△CQN≌△DMP(AAS),所以有QN=MP,CM=CN,即可求Q点坐标;
(3)由题意可求G(m,4-m),因此GQ与y轴垂直,由QG=GF,可求F(m,4-m-![]() m2),求出CF所在直线解析式为y=-(1+
m2),求出CF所在直线解析式为y=-(1+![]() m)x+4,确定点E(
m)x+4,确定点E(![]() ,4-m);过点E作ET垂直x轴,过点G作GS垂直PH,交PB于点S,可证明△ETB≌△HBP(HL),由平行的性质和等腰直角三角形的性质可知∠EGB=∠PGB=90°+45°=135°,得到△EGB≌△PGB(AAS),故有EG=PG,将点的坐标代入有m-
,4-m);过点E作ET垂直x轴,过点G作GS垂直PH,交PB于点S,可证明△ETB≌△HBP(HL),由平行的性质和等腰直角三角形的性质可知∠EGB=∠PGB=90°+45°=135°,得到△EGB≌△PGB(AAS),故有EG=PG,将点的坐标代入有m-![]() =-
=-![]() m2+m+4-(4-m),求出m即可.
m2+m+4-(4-m),求出m即可.
解:(1)由题意可知B(4,0),C(0,4),
∴CO=BO,
∴∠CBO=45°,
∵AD⊥BC,
∴∠DAO=45°,
∵A(-2,0),
∴AD的直线解析式为y=x+2;
(2)如图,过点P作x轴、y轴垂线,相交于点M,过点Q作y轴垂线,交于点N,

∵∠PCQ=90°,∠MCN=90°,
∴∠MCP=∠NCQ,
∵CP=CQ,∠CNQ=∠CMP=90°,
∴△CQN≌△DMP(AAS),
∴QN=MP,CM=CN
∵P的坐标为(m,-![]() m2+m+4),
m2+m+4),
∴CM=m,MP=4-(-![]() m2+m+4)=
m2+m+4)=![]() m2-m,
m2-m,
∴Q(-![]() m2+m,4-m);
m2+m,4-m);
(3)如图,

∵PH垂直于x轴,
∴G点横坐标为m,
∵G点在直线BC上,
∴G(m,4-m),
∵QG=GF,
∴![]() m2=4-m-yF,
m2=4-m-yF,
∴F(m,4-m-![]() m2)
m2)
∴CF所在直线解析式为y=-(1+![]() m)x+4,
m)x+4,
∴E(![]() ,4-m),
,4-m),
过点E作ET垂直x轴,过点G作GS垂直PH,交PB于点S,
∴ET=4-m,HB=4-m,
∴ET=HB,
∵BE=BP,
∴△ETB≌△HBP(HL),
∴∠EBT=∠BPH,
∵QG∥OB,
∴∠EBT=∠GEB,
∴∠GEB=∠BPG,
∠EGB=∠PGB=90°+45°=135°,
∴△EGB≌△PGB(AAS),
∴EG=PG,
∴m-![]() =-
=-![]() m2+m+4-(4-m),
m2+m+4-(4-m),
∴m=±![]() ,
,
∵P为直线BC右侧第一象限内一点,
∴m=![]() ,
,
∴P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,以
,以 为斜边作等腰直角
为斜边作等腰直角 ,连接
,连接 ,若
,若 ,
, ,则
,则 的长为______.
的长为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形
 中,点
中,点 是对角线
是对角线 的中点,
的中点, 过点
过点 与
与 ,
, 分别相交于
分别相交于 ,
, ,
, 过点
过点 与
与 ,
, 分别相交于点
分别相交于点 ,
, ,连接
,连接 ,
, ,
, ,
, .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)如图2,若
 ,
, ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形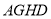 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形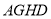 除外).
除外). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
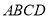 中,
中,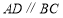 ,
,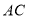 平分
平分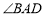 ,
,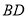 平分
平分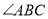 .
.(1)如下图,求证:四边形
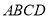 是菱形;
是菱形;(2)如下图,点
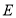 为四边形
为四边形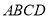 外一点,连接
外一点,连接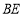 、
、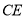 、
、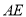 ,
,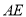 交
交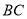 于点
于点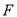 ,
,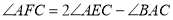 ,求证:
,求证: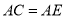 ;
;(3)如下图,在(2)的条件下,
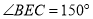 ,点
,点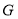 为
为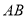 上一点,连接
上一点,连接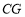 ,点
,点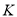 为
为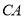 延长线上一点,
延长线上一点,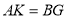 ,连接
,连接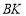 ,
,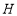 为
为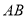 上一点,连接
上一点,连接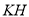 ,若
,若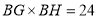 ,求
,求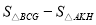 的值.
的值.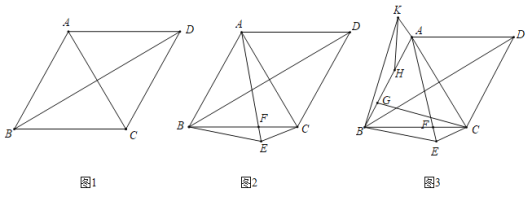
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点, ,将
,将 绕点
绕点 旋转至
旋转至 ,连接
,连接 ,
, 分别为
分别为 的中点,则
的中点,则 的最大值为_________.
的最大值为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题在该校校园内进行了随机调查.并将调查数据作出如下整理(未完整)


(1)本次调查共调查了 人(直接填空);
(2)请把整理的不完整图表补充完整;
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
相关试题

