【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
参考答案:
【答案】
(1)解:所求作△A1B1C如图所示:
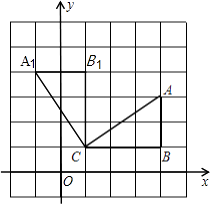
由A(4,3)、B(4,1)可建立如图所示坐标系,
则点A1的坐标为(﹣1,4),点B1的坐标为(1,4)
(2)解:∵AC= ![]() =
= ![]() =
= ![]() ,∠ACA1=90°
,∠ACA1=90°
∴在旋转过程中,△ABC所扫过的面积为:
S扇形CAA1+S△ABC
= ![]() +
+ ![]() ×3×2
×3×2
= ![]() +3.
+3.
【解析】(1)根据旋转中心旋转方向及旋转角度找出点A、B的对称点A1、B1的位置,然后顺次连接即可,根据A、B的坐标建立坐标系,据此写出点A1、B1的坐标;(2)用勾股定理得出AC的长度,在旋转过程中,△ABC所扫过的面积为:S扇形CAA1+S△ABC计算即可。
【考点精析】认真审题,首先需要了解扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形
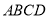 中,点
中,点 是对角线
是对角线 的中点,
的中点, 过点
过点 与
与 ,
, 分别相交于
分别相交于 ,
,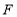 ,
, 过点
过点 与
与 ,
, 分别相交于点
分别相交于点 ,
, ,连接
,连接 ,
, ,
,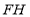 ,
, .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)如图2,若
 ,
, ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形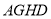 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形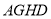 除外).
除外). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
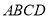 中,
中,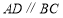 ,
,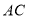 平分
平分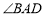 ,
,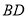 平分
平分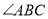 .
.(1)如下图,求证:四边形
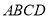 是菱形;
是菱形;(2)如下图,点
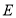 为四边形
为四边形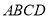 外一点,连接
外一点,连接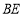 、
、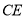 、
、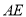 ,
,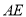 交
交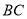 于点
于点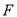 ,
,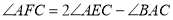 ,求证:
,求证: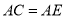 ;
;(3)如下图,在(2)的条件下,
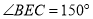 ,点
,点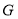 为
为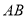 上一点,连接
上一点,连接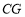 ,点
,点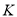 为
为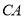 延长线上一点,
延长线上一点,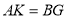 ,连接
,连接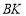 ,
,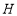 为
为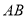 上一点,连接
上一点,连接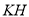 ,若
,若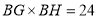 ,求
,求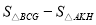 的值.
的值.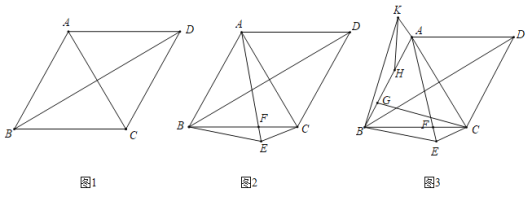
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
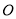 为坐标原点.直线
为坐标原点.直线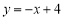 交
交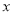 轴于点
轴于点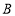 ,交
,交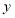 轴于点
轴于点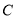 ,
,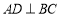 ,垂足为
,垂足为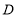 ,交
,交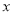 轴负半轴于点
轴负半轴于点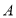 ,且点
,且点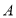 坐标为
坐标为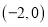 .
.(1)求直线
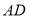 的解析式;
的解析式;(2)点
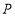 为直线
为直线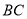 右侧第一象限内一点,连接
右侧第一象限内一点,连接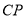 、
、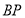 ,将线段
,将线段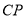 绕点
绕点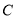 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段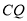 ,点
,点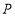 落在点
落在点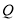 处,设点
处,设点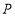 的坐标为
的坐标为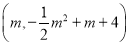 ,求点
,求点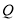 的坐标(用含
的坐标(用含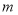 的式子表示);
的式子表示);(3)在(2)的条件下,过点
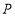 作
作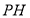 垂直于
垂直于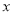 轴于点
轴于点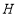 ,交
,交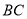 于点
于点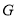 ,连接
,连接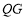 ,点
,点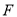 为
为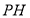 延长线上一点,连接
延长线上一点,连接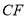 ,交
,交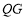 于点
于点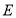 ,连接
,连接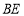 ,若
,若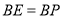 ,
,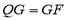 ,求点
,求点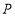 的坐标.
的坐标.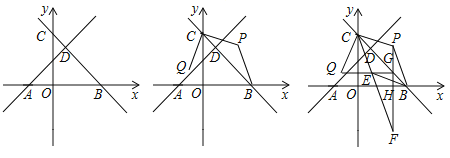
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
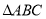 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点, ,将
,将 绕点
绕点 旋转至
旋转至 ,连接
,连接 ,
, 分别为
分别为 的中点,则
的中点,则 的最大值为_________.
的最大值为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题在该校校园内进行了随机调查.并将调查数据作出如下整理(未完整)


(1)本次调查共调查了 人(直接填空);
(2)请把整理的不完整图表补充完整;
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
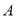 、
、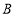 、
、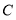 的坐标分别为
的坐标分别为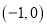 ,
,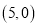 ,
,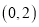 .若点
.若点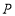 从
从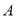 点出发,沿
点出发,沿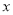 轴正方向以每秒1个单位长度的速度向
轴正方向以每秒1个单位长度的速度向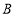 点移动,连接
点移动,连接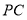 并延长到点
并延长到点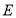 ,使
,使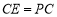 ,将线段
,将线段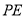 绕点
绕点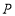 顺时针旋转
顺时针旋转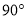 得到线段
得到线段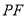 ,连接
,连接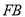 .若点
.若点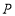 在移动的过程中,使
在移动的过程中,使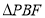 成为直角三角形,则点
成为直角三角形,则点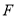 的坐标是__________.
的坐标是__________.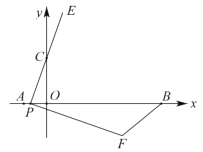
相关试题

