【题目】如图1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() ,
,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() ,
,![]() ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形![]() 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形![]() 除外).
除外).
参考答案:
【答案】(1)详见解析;(2)![]() 、
、![]() 、
、![]() 、
、![]()
【解析】
(1)由四边形ABCD是平行四边形,得到AD∥BC,根据平行四边形的性质得到∠EAO=∠FCO,证出△OAE≌△OCF,得到OE=OF,同理OG=OH,根据对角线互相平分的四边形是平行四边形得到结论;
(2)根据两组对边分别平行的四边形是平行四边形即可得到结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△OAE与△OCF中,
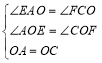
∴△OAE≌△OCF,
∴OE=OF,
同理OG=OH,
∴四边形EGFH是平行四边形;
(2)与四边形AGHD面积相等的所有平行四边形有GBCH,ABFE,EFCD,EGFH;
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∵EF∥AB,GH∥BC,
∴四边形GBCH,ABFE,EFCD,EGFH为平行四边形,
∵EF过点O,GH过点O,
∵OE=OF,OG=OH,
∴GBCH,ABFE,EFCD,EGFH,ACHD它们面积=![]() ABCD的面积,
ABCD的面积,
∴与四边形AGHD面积相等的所有平行四边形有GBCH,ABFE,EFCD,EGFH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,以
,以 为斜边作等腰直角
为斜边作等腰直角 ,连接
,连接 ,若
,若 ,
, ,则
,则 的长为______.
的长为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中,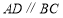 ,
,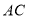 平分
平分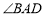 ,
,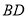 平分
平分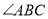 .
.(1)如下图,求证:四边形
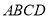 是菱形;
是菱形;(2)如下图,点
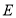 为四边形
为四边形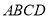 外一点,连接
外一点,连接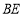 、
、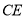 、
、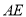 ,
,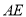 交
交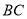 于点
于点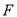 ,
,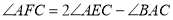 ,求证:
,求证: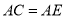 ;
;(3)如下图,在(2)的条件下,
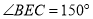 ,点
,点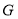 为
为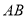 上一点,连接
上一点,连接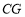 ,点
,点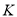 为
为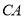 延长线上一点,
延长线上一点,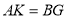 ,连接
,连接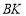 ,
,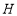 为
为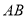 上一点,连接
上一点,连接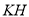 ,若
,若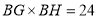 ,求
,求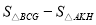 的值.
的值.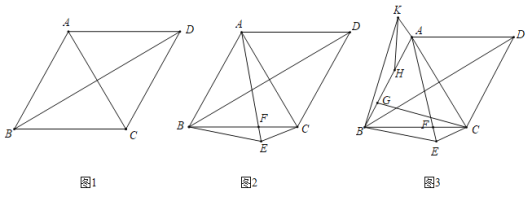
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为坐标原点.直线
为坐标原点.直线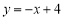 交
交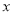 轴于点
轴于点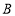 ,交
,交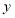 轴于点
轴于点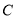 ,
,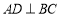 ,垂足为
,垂足为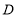 ,交
,交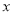 轴负半轴于点
轴负半轴于点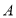 ,且点
,且点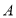 坐标为
坐标为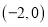 .
.(1)求直线
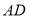 的解析式;
的解析式;(2)点
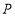 为直线
为直线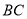 右侧第一象限内一点,连接
右侧第一象限内一点,连接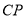 、
、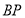 ,将线段
,将线段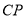 绕点
绕点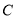 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段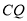 ,点
,点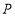 落在点
落在点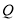 处,设点
处,设点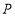 的坐标为
的坐标为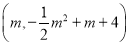 ,求点
,求点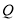 的坐标(用含
的坐标(用含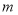 的式子表示);
的式子表示);(3)在(2)的条件下,过点
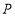 作
作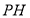 垂直于
垂直于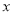 轴于点
轴于点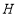 ,交
,交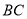 于点
于点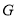 ,连接
,连接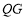 ,点
,点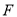 为
为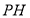 延长线上一点,连接
延长线上一点,连接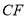 ,交
,交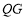 于点
于点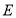 ,连接
,连接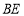 ,若
,若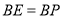 ,
,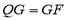 ,求点
,求点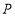 的坐标.
的坐标.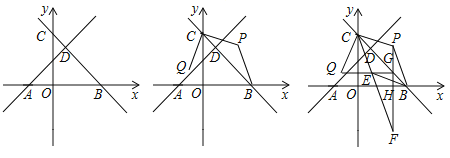
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
相关试题

