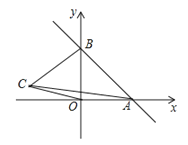
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
参考答案:
【答案】(1)一次函数解析式为y= -x+2 (2)a=![]() (3)存在,满足条件的点P的坐标为(0,0)或(22
(3)存在,满足条件的点P的坐标为(0,0)或(22![]() ,0)或(2
,0)或(2![]() +2,0)或(-2,0).
+2,0)或(-2,0).
【解析】
(1)根据勾股定理求出A、B两点坐标,利用待定系数法即可解决问题;
(2)根据S四边形ABCD=S△AOB+S△BOC计算即可,列出方程即可求出a的值;
(3)分三种情形讨论即可解决问题;
(1)在Rt△ABO中,∠OAB=45°,
∴∠OBA=∠OAB-∠OAB=90°-45°=45°
∴∠OBA=∠OAB
∴OA=OB
∴OB2+OA2=AB2即:2OB2=(2![]() )2,
)2,
∴OB=OA=2
∴点A(2,0),B(0,2).
∴![]()
解得:![]()
∴一次函数解析式为y= -x+2.
(2)如图,
∵S△AOB=![]() ×2×2=2,S△BOC=
×2×2=2,S△BOC=![]() ×2×|a|= -a,
×2×|a|= -a,
∴S四边形ABCD=S△AOB+S△BOC=2-a,
∵S△ABC=S四边形ABCO-S△AOC=2-a-![]() ×2×
×2×![]() =
=![]() -a,
-a,
当△ABC的面积与△ABO面积相等时,![]() a=2,解得a=
a=2,解得a=![]() .
.
(3)在x轴上,存在点P,使△PAB为等腰三角形
①当PA=PB时,P(0,0),
②当BP=BA时,P(-2,0),
③当AB=AP时,P(2-2![]() ,0)或(2+2
,0)或(2+2![]() ,0),
,0),
综上所述,满足条件的点P的坐标为(0,0)或(22![]() ,0)或(2
,0)或(2![]() +2,0)或(-2,0).
+2,0)或(-2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店将进货价为
 元的玩具以
元的玩具以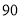 元的销售价售出,平均每月能售出
元的销售价售出,平均每月能售出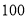 个市场调研表明:当销售价每涨价
个市场调研表明:当销售价每涨价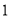 元时,其销售量将减少2个.
元时,其销售量将减少2个.(1)设每个玩具的销售价上涨
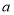 元,试用含
元,试用含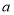 的式子填空:
的式子填空:①涨价后,每个玩具的销售价为 元;
②涨价后,每个玩具的利润为 元;
③涨价后,玩具的月销售量为 个.
(2)玩具店老板要想让该玩具的销售利润平均每月达到1600元,销售员甲说:“在原售价每个90元的基础上再上涨30元,可以完成任务”销售员乙说:“不用涨那么多,在原售价每个90元的基础上再上涨10元就可以了”判断销售员甲与销售员乙的说法是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段
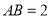 (单位长度),线段
(单位长度),线段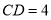 (单位长度),点
(单位长度),点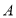 在数轴上表示的数是-10,点
在数轴上表示的数是-10,点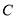 在数轴上表示的数是16,若线段
在数轴上表示的数是16,若线段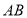 以每秒1个单位长度的速度向右匀速运动,同时线段
以每秒1个单位长度的速度向右匀速运动,同时线段 以每秒3个单位长度的速度向左匀速运动,设运动时间为
以每秒3个单位长度的速度向左匀速运动,设运动时间为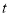 秒
秒(1)当点
 与点
与点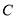 相遇时,点
相遇时,点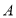 、点
、点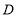 在数轴上表示的数分别为 ;
在数轴上表示的数分别为 ;(2)当
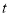 为何值时,点
为何值时,点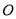 刚好是
刚好是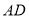 的中点
的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程,解答后面的问题:
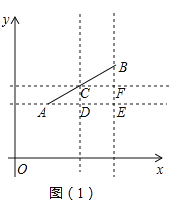
如图
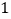 ,在平面直角坐标系
,在平面直角坐标系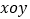 中,
中,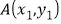 ,
,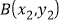 ,
, 为线段
为线段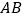 的中点,求
的中点,求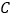 点的坐标;
点的坐标;解:分别过
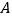 ,
,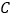 做
做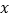 轴的平行线,过
轴的平行线,过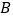 ,
,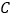 做
做 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图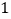 所示,设
所示,设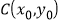 ,则
,则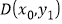 ,
,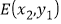 ,
,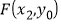
由图
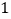 可知:
可知: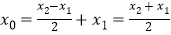
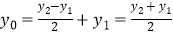
 线段
线段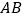 的中点
的中点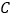 的坐标为
的坐标为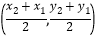
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知
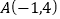 ,
,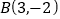 ,则线段
,则线段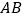 的中点坐标为
的中点坐标为(2)平行四边形
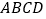 中,点
中,点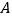 ,
,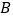 ,
,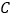 的坐标分别为
的坐标分别为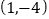 ,
,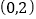 ,
,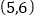 ,利用中点坐标公式求点
,利用中点坐标公式求点 的坐标。
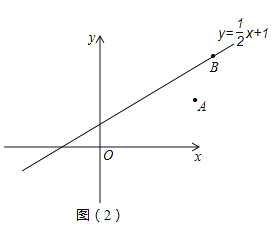
的坐标。(3)如图
 ,点
,点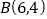 在函数
在函数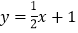 的图象上,
的图象上, 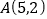 ,
,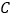 在
在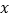 轴上,
轴上,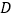 在函数
在函数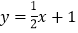 的图象上 ,以
的图象上 ,以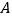 ,
,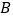 ,
,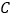 ,
,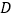 四个点为顶点,且以
四个点为顶点,且以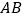 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的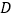 点坐标。
点坐标。 -
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线
 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.
(1)A,B两种型号的自行车的单价分别是多少?
(2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读材料:如图(1),在数轴上点
 示的数为
示的数为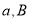 点表示的数为
点表示的数为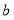 ,则点
,则点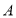 到点
到点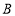 的距离记为
的距离记为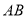 ,线段
,线段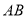 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即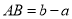
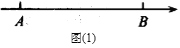
解决问题:如图(2),数轴上点
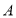 表示的数是
表示的数是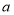 ,点
,点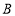 表示的数是
表示的数是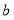 ,且有
,且有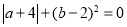 ,点
,点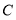 表示的数是
表示的数是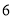 .
.
(1)若数轴上有一点
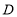 ,且
,且 ,则点
,则点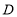 表示的数为______.
表示的数为______.(2)若点
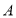 以每秒
以每秒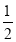 个单位长度的速度向左运动到
个单位长度的速度向左运动到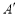 ,同时点
,同时点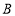 和点
和点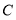 分别以每秒
分别以每秒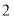 个单位长度和
个单位长度和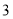 个单位长度的速度向右运动分别到
个单位长度的速度向右运动分别到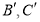 ,假设
,假设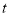 秒钟过后,若点
秒钟过后,若点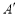 与点
与点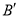 之间的距离表示为
之间的距离表示为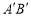 ,点
,点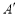 与点
与点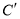 之间的距离表示为
之间的距离表示为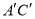 ,点
,点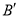 与点
与点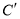 之间的距离表示为
之间的距离表示为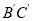 .则点
.则点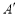 表示的数是______,
表示的数是______,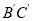 =________
=________ 用含
用含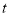 的式子表示
的式子表示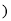 .
.(3)请问:
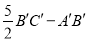 的值是否随着时间
的值是否随着时间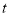 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.(4)若点
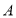 点
点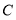 分别以
分别以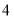 个单位每秒和
个单位每秒和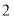 个单位每秒的速度相向而行,则几秒后A、C两点相距
个单位每秒的速度相向而行,则几秒后A、C两点相距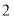 个单位长度?
个单位长度?
相关试题

