【题目】先阅读材料:如图(1),在数轴上点![]() 示的数为
示的数为![]() 点表示的数为
点表示的数为![]() ,则点
,则点![]() 到点
到点![]() 的距离记为
的距离记为![]() ,线段
,线段![]() 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即![]()
![]()
解决问题:如图(2),数轴上点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,且有
,且有![]() ,点
,点![]() 表示的数是
表示的数是![]() .
.
![]()
(1)若数轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 表示的数为______.
表示的数为______.
(2)若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动到
个单位长度的速度向左运动到![]() ,同时点
,同时点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动分别到
个单位长度的速度向右运动分别到![]() ,假设
,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .则点
.则点![]() 表示的数是______,
表示的数是______,![]() =________
=________![]() 用含
用含![]() 的式子表示
的式子表示![]() .
.
(3)请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
(4)若点![]() 点
点![]() 分别以
分别以![]() 个单位每秒和
个单位每秒和![]() 个单位每秒的速度相向而行,则几秒后A、C两点相距
个单位每秒的速度相向而行,则几秒后A、C两点相距![]() 个单位长度?
个单位长度?
参考答案:
【答案】(1)-7或-1;(2)-4-![]() t,4+t;(3)不变,定值为4;(4)t=2或t=
t,4+t;(3)不变,定值为4;(4)t=2或t=![]() .
.
【解析】
(1)根据非负数的性质求出a、b的值,再由距离的定义求解即可;
(2)根据题意表示出点![]() 、
、![]() 、
、![]() 所表示的数,即可得出结论;
所表示的数,即可得出结论;
(3)先求出![]() ,然后代入化简即可得出结论;
,然后代入化简即可得出结论;
(4)求出点A的路程为4t,点C的路程为2t,然后分为相遇前相距![]() 个单位长度和相遇后相距
个单位长度和相遇后相距![]() 个单位长度列方程,求解即可.
个单位长度列方程,求解即可.
(1)由非负数的性质可得到:a+4=0,b-2=0,解得:a=-4,b=2.
设D表示的数为x,则AD=x-(-4)=3或-4-x=3,解得:x=-1或x=-7.
故答案为:-7或-1.
(2)由题意可知:点![]() 表示的数是:
表示的数是:![]() ,点
,点![]() 表示的数是:
表示的数是:![]() ,点
,点![]() 表示的数是:
表示的数是:![]() ,∴
,∴![]() =
=![]() -(
-(![]() )=
)=![]() =
=![]() .
.
故答案为:![]() ,
,![]() .
.
(3)由(2)得:![]() =
= ![]() -(
-(![]() )=
)=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =4.故
=4.故![]() 为定值4.
为定值4.
(4)由题意得:点A的路程为4t,点C的路程为2t,∴4t+2t=10+2或4t+2t=10-2,解得:t=2或t=![]() .
.
-
科目: 来源: 题型:
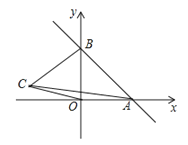
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2
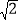 ,∠OAB=45°
,∠OAB=45°(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,
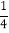 );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值; (3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线
 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.
(1)A,B两种型号的自行车的单价分别是多少?
(2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
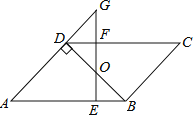
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有______.
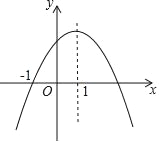
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
相关试题

