Question

【题目】在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。

（1）写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由；
（2）如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

Answer 1

【答案】
（1） 解：∵∠BAC=90°，O为BC的中点，

∴BO=CO=AO=BC，

（2）解：△OMN是等腰直角三角形.理由如下：

连接OA，如图，

∵AC=AB，∠BAC=90°，
∴OA=OB=OC，OA平分∠BAC，∠B=45°，

∴∠NAO=∠B=45°，

在△NAO和△MBO 中，

AN=BM ，∠NAO=∠B ，AO=BO ，

∴△NAO≌ △MBO，
∴ON=OM，∠AON=∠BOM，

∵AC=AB，O是BC的中点，
∴AO⊥BC，

即∠BOM+∠AOM=90°，
∴∠AON+∠AOM=90°，

即∠NOM=90°，

∴△OMN是等腰直角三角形.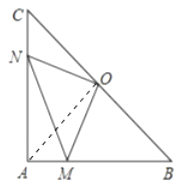

【解析】（1）根据直角三角形斜边上的中线等于斜边的一边得出答案.
（2）△OMN是等腰直角三角形.理由如下：连接OA，由等腰直角三角形性质得出OA=OB=OC，AO⊥BC，OA平分∠BAC，∠NAO=∠B=45°，再由SAS得到△NAO≌ △MBO，由全等三角形的性质得出ON=OM，∠AON=∠BOM，再根据垂直的定义得出∠BOM+∠AOM=90°，由等量代换得∠NOM=90°，从而得证.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°，以及对直角三角形斜边上的中线的理解，了解直角三角形斜边上的中线等于斜边的一半．