【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 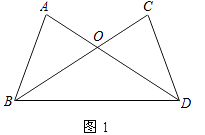
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 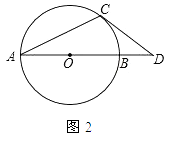
参考答案:
【答案】
(1)证明:∵∠OBD=∠ODB,
∴OB=OD,
在△AOB与△COD中, 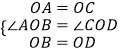 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD
(2)解:连接OC,如图所示:

∵CD与⊙O相切,
∴OC⊥CD,
∵OA=OC,OA=1,
∴OC=1,
∴CD= ![]() =
= ![]() =1,
=1,
∴CD=OC,
∴△OCD为等腰直角三角形,
∴∠COB=45°,
∴∠BAC= ![]() ∠COB=22.5°.
∠COB=22.5°.
【解析】(1)由∠OBD=∠ODB,得出OB=OD,再由SAS证得△AOB≌△COD,即可得出结论;(2)连接OC,由CD与⊙O相切,得出OC⊥CD,求出CD=1,得出△OCD为等腰直角三角形,推出∠COD=45°,即可得出结果.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=
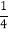 ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.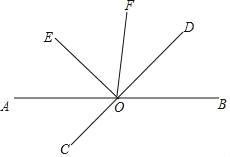
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:3+2=3×2-1,4+
 =4×
=4× -1,给出定义如下:
-1,给出定义如下:我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,
 )都是“椒江有理数对”.
)都是“椒江有理数对”.(1)数对(-2,1),(5,
 )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段 AB=10cm,直线 AB 上有一点 C,且 BC=4cm,M 是线段 AC 的中点,则 AM 的长( )
A. 7cm B. 3cm C. 3cm 或 7cm D. 7cm 或 9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 如图,在
如图,在 中,
中,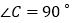 ,
,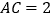 ,
, ,可求得
,可求得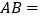 ______.
______.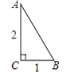
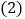 如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点
如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点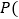 滚动时与点O重合
滚动时与点O重合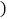 由原点到达点
由原点到达点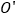 ,则
,则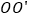 的长度是______.
的长度是______.
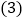 如图,
如图, 是一个等腰直角三角形,它的面积是2,把它沿着斜边的高线剪开拼成如图正方形EBDC,则这个正方形的边长是______.
是一个等腰直角三角形,它的面积是2,把它沿着斜边的高线剪开拼成如图正方形EBDC,则这个正方形的边长是______.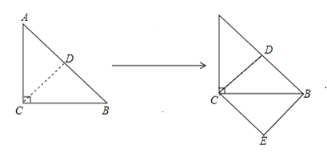
 请你在
请你在 的网格图中
的网格图中 每个小正方形边长均为
每个小正方形边长均为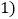 ,画出一条长为
,画出一条长为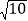 的线段;
的线段;
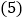 学习了实数后,我们知道数轴上的点与实数是一一对应的关系
学习了实数后,我们知道数轴上的点与实数是一一对应的关系 那么请你在图的数轴上画出表示
那么请你在图的数轴上画出表示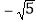 的点
的点 保留作图痕迹
保留作图痕迹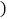 .
.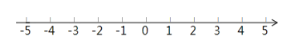
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,A、B、C分别为数轴上的三点,A点对应的数为-200,B点对应的数为-20,C点对应的数为40.甲从C点出发,以6单位/秒的速度向左运动.
(1)当甲在B点、C点之间运动时,设运时间为x秒,请用x的代数式表示:
甲到A点的距离: ;
甲到B点的距离: ;
甲到C点的距离: .
(2)当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向右运动,设两人在数轴上的D点相遇,求D点对应的数;
(3)若当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向左运动,设两人在数轴上的E点相遇,求E点对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为8,高AE长为
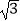 ,则AC:BD=( )
,则AC:BD=( ) 
A.1:2
B.1:3
C.1: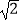
D.1: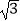
相关试题

