【题目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当OB绕点O在
当OB绕点O在![]() 内旋转时,则
内旋转时,则![]() 的大小为______;
的大小为______;
![]() 如图2,若
如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 当
当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小;
的大小;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 内绕着点O以
内绕着点O以![]() 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时,![]() 和
和![]() 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值

参考答案:
【答案】(1)78°;(2)∠MON=66°;(3)当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.
【解析】
(1)由角平分线的定义可得∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON,即可求∠MON的大小;
∠BON,即可求∠MON的大小;
(2)由角平分线的定义可得∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,即可求∠MON的大小;
∠BOD,即可求∠MON的大小;
(3)由题意可得∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t,分∠AOM=2∠DON,∠DON=2∠AOM两种情况讨论,列出方程可求t的值.
(1)∵OM平分∠AOB,ON平分∠BOD,∴∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON.
∠BON.
∵∠MON=∠BOM+∠BON![]() ∠AOD,∴∠MON=78°.
∠AOD,∴∠MON=78°.
故答案为:78°.
(2)∵OM平分∠AOC,ON平分∠BOD,∴∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC
∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC![]() ∠AOC
∠AOC![]() ∠BOD﹣24°
∠BOD﹣24°![]() (∠AOC+∠BOD)﹣24°,∴∠MON
(∠AOC+∠BOD)﹣24°,∴∠MON![]() (∠AOD+∠BOC)﹣24°
(∠AOD+∠BOC)﹣24°![]() 180°﹣24°=66°.
180°﹣24°=66°.
(3)∵∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒,OM平分∠AOC,ON平分∠BOD,∴∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t.
若∠AOM=2∠DON时,即27+t=2(63﹣t),∴t=33;
若2∠AOM=∠DON,即2(27+t)=63﹣t,∴t=3.
综上所述:当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a= ;③ac=b﹣1;④
;③ac=b﹣1;④ 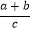 >0
>0
其中正确的个数有( )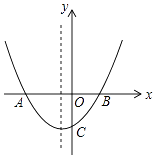
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
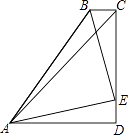
A.
B.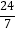
C.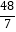
D.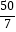
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A、B、C、D四个等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:

(1)抽取了__名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是__;
(4)若A、B、C三个等级为合格,该校初二年级有900名学生,估计全年级生物合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2
 ,点D为AC与反比例函数y=
,点D为AC与反比例函数y= 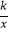 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 .
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 . 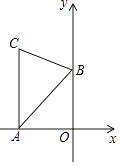
-
科目: 来源: 题型:
查看答案和解析>>【题目】用矩形纸片折出直角的平分线,下列折法正确的是( )
A.
B.
C.
D.
相关试题

