Question

【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD.

（1）求证：四边形OCED是菱形；

（2）若AB＝3，BC＝4，求四边形OCED的面积．

Answer 1

【答案】（1）见解析；（2）6

【解析】试题分析：

(1) 观察题目中的两组平行线易知，四边形OCED的两组对边分别平行，即四边形OCED是平行四边形. 在平行四边形的基础上若想证明其为菱形，则要么再证一组邻边相等要么再证对角线互相垂直. 继续观察图形可知，利用矩形ABCD的性质证明OC与OD相等是容易的. 因此，根据一组邻边相等的平行四边形为菱形即可证明四边形OCED是菱形.

(2) 分析条件可知，在矩形ABCD中，AB=CD=3，线段CD恰好是菱形OCED的一条对角线，于是容易想到利用对角线乘积的一半去计算菱形的面积. 作出菱形的另一条对角线OE，利用菱形OCED的性质和矩形ABCD的性质可知OE∥BC，进而得到四边形OBCE为平行四边形，再利用平行四边形的性质可求得OE的长度. 在得到两条对角线的长度后，按菱形的面积公式即可得到四边形OCED的面积.

试题解析：

(1) 证明：∵DE∥AC，CE∥BD，

∴四边形OCED是平行四边形，

∵四边形ABCD是矩形，

∴OC= ，OD= ，AC=BD，

∴OC=OD，

∴平行四边形OCED为菱形.

(2) 四边形OCED的面积为6. 求解过程如下.

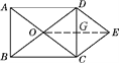
连接OE，交CD于点G. (如图)

∵四边形OCED为菱形，

∴OE⊥CD，

∴∠OGD=90°，

∵四边形ABCD为矩形，

∴∠BCD=90°，

∴∠OGD=∠BCD，

∴OE∥BC，

∵CE∥BD，OE∥BC，

∴四边形OBCE为平行四边形，

∴OE=BC，

∵四边形ABCD为矩形，

∴CD=AB，

∵AB=3，BC=4，

∴CD=AB=3，OE=BC =4，

∴菱形OCED的面积为，

即四边形OCED的面积为6.