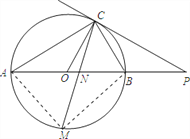
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、8.
【解析】试题分析:(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP,故PC是⊙O的切线;
(2)AB是直径;故只需证明BC与半径相等即可;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC,代入数据可得MNMC=BM2=8.
试题解析:(1)∵OA=OC,∴∠A=∠ACO,
又∵∠COB=2∠A,∠COB=2∠PCB,∴∠A=∠ACO=∠PCB,
又∵AB是⊙O的直径,∴∠ACO+∠OCB=90°,∴∠PCB+∠OCB=90°,
即OC⊥CP,
∵OC是⊙O的半径,∴PC是⊙O的切线;
(2)∵AC=PC,∴∠A=∠P,∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,∴∠COB=∠CBO,∴BC=OC,
∴![]() ;
;
(3)连接MA,MB,
∵点M是弧AB的中点,∴ 弧AM=弧BM,∴∠ACM=∠BCM,
∵∠ACM=∠ABM,∴∠BCM=∠ABM,
∵∠BMN=∠BMC,∴△MBN∽△MCB,∴ ![]() ,∴
,∴![]() ,
,
又∵AB是⊙O的直径,弧AM=弧BM,
∴∠AMB=90°,AM=BM,
∵AB=4,∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
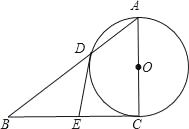
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
(1)求证:DE=
 BC;
BC;(2)若四边形ODEC是正方形,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小亮、小刚、小颖一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有________个人的说法是正确的.( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=﹣
 x+1,直线AC交x轴于点C,交y轴于点A.
x+1,直线AC交x轴于点C,交y轴于点A.(1)若等边△OBD的顶点D与点C重合,另一顶点B在第一象限内,直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元二次方程ax2+bx+c=0(a≠0)满足4a-2b+c=0,且有两个相等的实数根,则( )
A. b=aB. c=2aC. a(x+2)2=0(a≠0)D. a(x-2)2=0(a≠0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 的对角线
的对角线 和
和 交于点
交于点 ,则下列不能判断四边形
,则下列不能判断四边形 是平行四边形的条件是( )
是平行四边形的条件是( )
A.
 ,
, ∥
∥
B.∠
 =∠
=∠ ,
, ∥
∥
C.
 ,
, =
=
D.∠
 =∠
=∠ ,∠
,∠ =∠
=∠
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:

(1)填表:
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)当三角形的个数为
 时,火柴棒的根数是多少?
时,火柴棒的根数是多少?(3)求当
 时,有多少根火柴棒?
时,有多少根火柴棒?(4)当火柴棒的根数为2017时,三角形的个数是多少?
相关试题

