Question

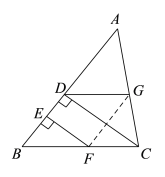
【题目】小明、小亮、小刚、小颖一起研究一道数学题．如图，已知EF⊥AB，CD⊥AB.

小明说：“如果还知道∠CDG＝∠BFE，那么能得到∠AGD＝∠ACB.”

小亮说：“把小明的已知和结论倒过来，即由∠AGD＝∠ACB，可得到∠CDG＝∠BFE.”

小刚说：“∠AGD一定大于∠BFE.”

小颖说：“如果连结GF，那么GF一定平行于AB.”

他们四人中，有________个人的说法是正确的．(　　)

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】B

【解析】

根据“垂直的定义、平行线的判定与性质”结合“已知条件”进行分析判断即可.

（1）∵EF⊥AB，CD⊥AB，

∴∠BEF=∠BDC=90°，

∴CD∥EF，

∴∠BFE=∠BCD，

∵∠CDG=∠BFE，

∴∠CDG=∠BCD，

∴DG∥BC，

∴∠AGD=∠ACB，即小明的说法正确；

（2）∵∠AGD=∠ACB，

∴DG∥BC，

∴∠CDG=∠BFE，

∵EF⊥AB，CD⊥AB，

∴∠BEF=∠BDC=90°，

∴CD∥EF，

∴∠BFE=∠BCD，

∴∠CDG=∠BFE，即小亮的说法正确；

（3）∵EF⊥AB，CD⊥AB，

∴∠BEF=∠BDC=90°，

∴CD∥EF，

∴∠BFE=∠BCD，

∵∠ACB>∠BCD，

∴∠ACB>∠BFE，

但由于不知道此时DG与BC的位置关系，不能确定∠AGD与∠ACB的大小关系，

∴∠AGD一定大于∠BFE的说法不一定成立，即小刚的说法错误；

（4）如下图，连接GF，

因为由已知条件不能确定点F、G在BC和AC上的位置，

所以不能确定FG与AB的位置关系，即小颖的说法错误.

综上所述，四人的说法中，有二人的说法是正确的.

故选B.