【题目】如图,直线AB、CD相交于点0,OE平分∠BOD,OF平分∠COE.∠BOF=30°,求:(1)∠EOD的度数;(2)∠AOC的度数.

参考答案:
【答案】(1)∠EOD=40°;(2)∠AOC=80°.
【解析】
(1)根据OE平分∠BOD,可得∠BOE=∠DOE,设∠BOE=∠DOE=x,再根据OF平分∠COE,得到∠EOF=![]() ∠COE=90°﹣
∠COE=90°﹣![]() x,再根据∠BOF=30°列出方程即可;
x,再根据∠BOF=30°列出方程即可;
(2)利用对顶角定义计算即可求出所求.
(1)∵OE平分∠BOD,
∴∠BOE=∠DOE,
设∠BOE=∠DOE=x,则有∠COE=180°﹣x,
∵OF平分∠COE,
∴∠EOF=![]() (180°﹣x)=90°﹣
(180°﹣x)=90°﹣![]() x,
x,
由题意得:∠EOF﹣∠BOE=30°,即90°﹣![]() x﹣x=30°,
x﹣x=30°,
解得:x=40°,
则∠EOD=40°
(2)∵∠EOD=40°,OE平分∠BOD;
∴∠AOC=∠BOD=2∠EOD =80°.
-
科目: 来源: 题型:
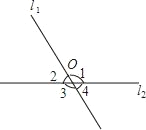
查看答案和解析>>【题目】如图所示,直线l1与l2相交于点O,且∠1+∠3=2(∠2+∠4),求下列角的度数.(1)∠2+∠4;(2)∠1,∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列结论正确的个数是( ) ①m+n>0;②m﹣n>0;③mn<0;④|m﹣n|=m﹣n.
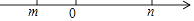
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( )
DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( ) 
A.∠1=∠2
B.S△OCE=S△OCD
C.OD=CD
D.OC垂直平分DE -
科目: 来源: 题型:
查看答案和解析>>【题目】常数a,b,c在数轴上的位置如图所示,则关于x的一元二次方程ax2+bx+c=0根的情况是( )

A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定 -
科目: 来源: 题型:
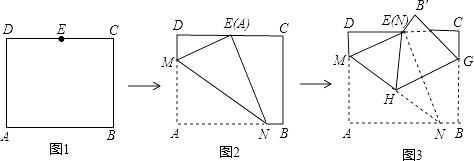
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8
 ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG= 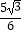
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD平移后得到四边形A′B′C′D′
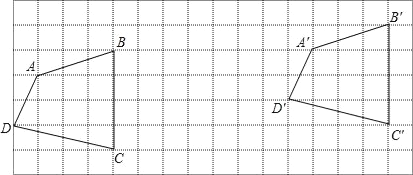
观察图形后完成下列问题:
(1)四边形ABCD先向 平移 个格,再向 平移 个格后得到四边形A′B′C′D′.
(2)图中有哪些相等的线段?有哪些平行的线段?
(3)S四边形ABCD和S四边形A′B′C′D′有什么关系?
相关试题

