【题目】如图,在矩形ABCD中,AB=8 ![]() ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG= ![]()
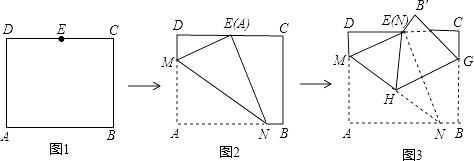
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
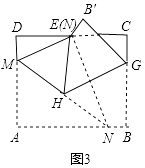
【解析】解:如图3,由折叠可得,∠MEN=∠A=90°,HG⊥NE, 即ME⊥EN,HG⊥EN,
∴EM∥GH,故①正确;
∴∠NME=∠NHG,
由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,
∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.
设DM=x,则AM=EM=10﹣x,
∵点E是CD的中点,AB=CD=8 ![]() ,
,
∴DE= ![]() CD=4
CD=4 ![]() ,
,
在Rt△DEM中,∵DM2+DE2=EM2 ,
∴(4 ![]() )2+x2=(10﹣x)2 ,
)2+x2=(10﹣x)2 ,
解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,
∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EN= ![]() ,
,
∴AN= ![]() ,
,
∴tan∠AMN= ![]() =
= ![]() ,
,
∴tan∠EHG= ![]() ,故④正确;
,故④正确;
又∵tan60°= ![]() >
> ![]() ,
,
∴∠AMN≠60°,即∠EMH≠60°,
∴△MEH不是等边三角形,故②错误.
∴正确的结论有3个.
故选:C.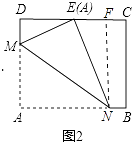
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( )
DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( ) 
A.∠1=∠2
B.S△OCE=S△OCD
C.OD=CD
D.OC垂直平分DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点0,OE平分∠BOD,OF平分∠COE.∠BOF=30°,求:(1)∠EOD的度数;(2)∠AOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】常数a,b,c在数轴上的位置如图所示,则关于x的一元二次方程ax2+bx+c=0根的情况是( )

A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD平移后得到四边形A′B′C′D′
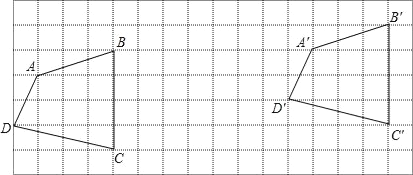
观察图形后完成下列问题:
(1)四边形ABCD先向 平移 个格,再向 平移 个格后得到四边形A′B′C′D′.
(2)图中有哪些相等的线段?有哪些平行的线段?
(3)S四边形ABCD和S四边形A′B′C′D′有什么关系?
-
科目: 来源: 题型:
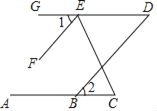
查看答案和解析>>【题目】如图,已知∠1=∠2=50°,EF∥DB.
(1)DG与AB平行吗?请说明理由.
(2)若EC平分∠FED,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为 .
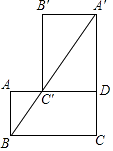
相关试题

