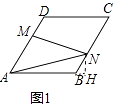
【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= ![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.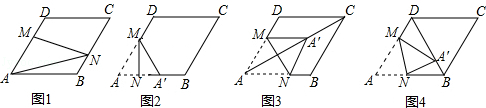
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到
△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ![]() ;
;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)![]()
(2)
①1
②在菱形ABCD中,∠A=60°,
∴∠DAC=∠BAC=30°,
∵点A′落在对角线AC上,
∴MN⊥AC,
∴∠AMN=∠ANM=60°,
∴AM=AN,
由折叠的性质可知,AM=AN=A′M=A′N,
∴四边形AM A′N是菱形;
③∠A′=∠A=60°,
∴∠BA′N+∠DA′M=120°,又∠DMA′+∠DA′M=120°,
∴∠BA′N=∠DMA′,又∠A′DM=∠NBA′,
∴△A′DM∽△NBA′,
∴ ![]() =
= ![]() =
= ![]() =2.
=2.
【解析】解:(1)作NH⊥AB交AB的延长线于H,
∵AD=3,
∴DM= ![]() AD=1,AM=2,
AD=1,AM=2,
∵菱形的中心对称图形,MN过对角线AC与BD的交点,
∴BN=DM=1,
∵∠DAB=60°,
∴∠NBH=60°,
∴BH= ![]() BN=
BN= ![]() ,NH=
,NH= ![]() BN=
BN= ![]() ,
,
∴AN= ![]() =
= ![]() ,
,
故答案为: ![]() ;
;
⑵①∵点A′落在AB边上,
∴MN⊥AA′,
∴AN= ![]() AM=1,
AM=1,
故答案为:1;
(1)作NH⊥AB交AB的延长线于H,根据题意求出DM、AM,根据菱形的中心对称图形得到BN=DM=1,根据直角三角形的性质求出BH、NH,根据勾股定理计算;(2)①根据直角三角形的性质计算;②根据翻转变换的性质、菱形的判定定理进行证明;③证明△A′DM∽△NBA′,根据相似三角形的性质计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.

(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:

(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数
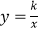 的图象上.
的图象上.
(1)求m,k的值;
(2)求直线AB的函数表达式;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,直接写出点M,N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,种植花卉的利润y2与投资成本x的平方成正比例关系,并得到了表格中的数据;
投资量x(万元)
2
种植树木的利润y1(万元)
4
种植花卉的利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户计划以8万元资金投入种植花卉和树木,设他投入种植花卉金额万元,种植花卉和树木共获利润W万元,求出W与m之间的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万元,在(2)的条件下,求出投资种植花卉的金额m的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④当y>0时,x的取值范围是﹣1<x<3;⑤当x>0时,y随x增大而减小.其中结论正确的个数是( )

A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=
 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( ) 
A.
B.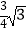
C.
D.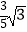
相关试题

