【题目】如图1,在平面直角坐标系中,△OAB是等边三角形,点B的坐标为(4,0),点C(a,0)是x轴上一动点,其中a≠0,将△AOC绕点A逆时针方向旋转60°得到△ABD,连接CD.
(1)求证;△ACD是等边三角形;
(2)如图2,当0<a<4时,△BCD周长是否存在最小值?若存在,求出a的值;若不存在,请说明理由.
(3)如图3,当点C在x轴上运动时,是否存在以B、C、D为顶点的三角形是直角三角形?若存在,求出a的值;若不存在,请说明理由.

参考答案:
【答案】(1)详见解析;(2)存在,a=2;(3)a=8.
【解析】
(1)根据旋转变换的性质、等边三角形的判定定理证明;
(2)证明△OAC≌△BAD,根据全等三角形的性质得到BD=OC,根据等边三角形的性质计算即可;
(3)分点C在x轴的负半轴上、点C在线段OB上、点C在点B的右侧三种情况,根据直角三角形的性质计算.
(1)证明:由旋转变换的性质可知,AC=AD,∠CAD=60°,
∴ACD是等边三角形;
(2)解:存在,a=2,
理由如下:∵△OAB和△ACD都是等边三角形,
∴AO=AB,AC=AD,∠OAB=∠CAD=60°,
∴∠OAB-∠CAB=∠CAD-∠CAB,即∠OAC=∠BAD,
在△OAC和△BAD中,
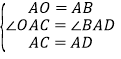 ,
,
∴△OAC≌△BAD(SAS)
∴BD=OC,
∴△BCD周长=BC+BD+CD=BC+OC+CD=OB+CD,
当CD最小时,△BCD周长最小,
∵ACD是等边三角形,
∴CD=AC,
当AC⊥OB时,即OC=2,AC最小,最小值为![]() =2
=2![]() ,
,
∴△BCD周长的最小值为4+2![]() ,此时a=2;
,此时a=2;
(3)解:当点C在x轴的负半轴上时,∠BDC=90°,
则∠ADB=30°,
∵△OAC≌△BAD,
∴∠ACO=∠ADB=30°,
∴∠BCD=30°,
∴BD=![]() BC,
BC,
∴OC=![]() BC,
BC,
∴OC=4,
则a=-4;
当点C在线段OB上时,∠DBC=120°,
∴不存在以B、C、D为顶点的三角形是直角三角形,
∴a不存在;
当点C在点B的右侧时,∠BCD=90°,
则∠ACO=30°,
∵∠AOC=60°,
∴∠OAC=90°,又∠ACO=30°,
∴OC=2OA=8,
∴a=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年8月高邮高铁将通车,高邮至北京的路程约为900km,甲、乙两人从高邮出发,分别乘坐汽车A与高铁B前往北京.已知A车的平均速度比B车的平均速度慢150km/h,A车的行驶时间是B车的行驶时间的2.5倍,两车的行驶时间分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为
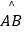 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.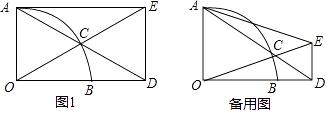
(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一项工程,甲单独做需要10天能完成,乙单独做需要15天能完成,甲做一天需要的报酬比乙做一天需要的报酬多100元,甲、乙合作完成此项工程需要5400元报酬.
(1)问甲、乙合作多少天能完成此项工程?
(2)求甲做一天需要的报酬;
(3)为了节省开支,应在甲单独完成、乙单独完成、甲乙合作完成这三种方案中选择哪种方案?请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

