【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?


参考答案:
【答案】(1)大棚的宽为14米,长为8米;(2)选择方案二更好.
【解析】分析:(1)设大棚的宽为a米,长为b米,分别利用大棚的周长为44米,长比宽多6米,分别得出等式求出答案;
(2)分别求出两种方案的造价进而得出答案.
详解:(1)设大棚的宽为a米,长为b米,根据题意可得:
![]() ,解得:
,解得:![]() ,
,
答:大棚的宽为14米,长为8米;
(2)大棚的面积为:2×14×8=224(平方米),
若按照方案一计算,大棚的造价为:224×60500=12940(元),
若按照方案二计算,大棚的造价为:224×70(120%)=12544(元)
显然:12544<12940,所以选择方案二更好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中,且A
 、B
、B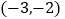 、C
、C .将其平移后得到
.将其平移后得到 ,若A,B的对应点是
,若A,B的对应点是 ,
, ,C的对应点
,C的对应点 的坐标是
的坐标是 .
.(1)在平面直角坐标系中画出△ABC;
(2)写出点
 的坐标是_____________,
的坐标是_____________, 坐标是___________;
坐标是___________;(3)此次平移也可看作
 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
 .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积. -
科目: 来源: 题型:
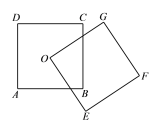
查看答案和解析>>【题目】如图所示,正方形ABCD和正方形OEFG的边长均为5,O为正方形ABCD的中心,则图中重叠部分的面积是 _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
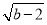 =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
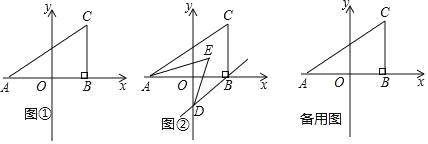
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.

(1)求证:DC=DE;
(2)若tan∠CAB= ,AB=3,求BD的长.
,AB=3,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
相关试题

