搜索
【题目】2020年8月高邮高铁将通车，高邮至北京的路程约为900km，甲、乙两人从高邮出发，分别乘坐汽车A与高铁B前往北京．已知A车的平均速度比B车的平均速度慢150km/h，A车的行驶时间是B车的行驶时间的2.5倍，两车的行驶时间分别为多少？
参考答案：
【答案】A车行驶的时间为9小时，B车行驶的时间为3.6小时．
【解析】
设B车行驶的时间为t小时，则A车行驶的时间为2.5t小时，根据平均速度=路程÷时间结合A车的平均速度比B车的平均速度慢150km/h，即可得出关于t的分式方程，解之经检验后即可得出结论．
解：设B车行驶的时间为t小时，则A车行驶的时间为2.5t小时，
根据题意得：
，
解得：t=3.6，
经检验，t=3.6是原分式方程的解，且符合题意，
∴2.5t=9．
答：A车行驶的时间为9小时，B车行驶的时间为3.6小时．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，AD平分∠BAC，
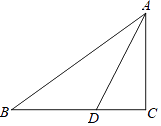
（1）求作⊙O，圆心O是AD的中垂线与AB的交点，OD为半径．（尺规作图，不写作法，保留痕迹）
（2）求证：BC是⊙O切线．
（3）若BD=5，DC=3，求AC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校为学生开展拓展性课程，拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区（如图1），要求两个大棚之间有间隔4米的路，设计方案如图2，已知每个大棚的周长为44米．
（1）求每个大棚的长和宽各是多少？
（2）现有两种大棚造价的方案，方案一是每平方米60元，超过100平方米优惠500元，方案二是每平方米70元，超过100平方米优惠总价的20%，试问选择哪种方案更优惠？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=
x+4与x轴相交于点A，与y轴相交于点B．（1）求△AOB的面积；
（2）过B点作直线BC与x轴相交于点C，若△ABC的面积是16，求点C的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，△OAB是等边三角形，点B的坐标为（4，0），点C（a，0）是x轴上一动点，其中a≠0，将△AOC绕点A逆时针方向旋转60°得到△ABD，连接CD．
（1）求证；△ACD是等边三角形；
（2）如图2，当0＜a＜4时，△BCD周长是否存在最小值？若存在，求出a的值；若不存在，请说明理由．
（3）如图3，当点C在x轴上运动时，是否存在以B、C、D为顶点的三角形是直角三角形？若存在，求出a的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：以O为圆心的扇形AOB中，∠AOB=90°，点C为
上一动点，射线AC交射线OB于点D，过点D作OD的垂线交射线OC于点E，联结AE．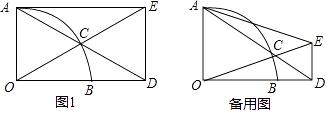
（1）如图1，当四边形AODE为矩形时，求∠ADO的度数；
（2）当扇形的半径长为5，且AC=6时，求线段DE的长；
（3）联结BC，试问：在点C运动的过程中，∠BCD的大小是否确定？若是，请求出它的度数；若不是，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】现有一项工程，甲单独做需要10天能完成，乙单独做需要15天能完成，甲做一天需要的报酬比乙做一天需要的报酬多100元，甲、乙合作完成此项工程需要5400元报酬．
（1）问甲、乙合作多少天能完成此项工程？
（2）求甲做一天需要的报酬；
（3）为了节省开支，应在甲单独完成、乙单独完成、甲乙合作完成这三种方案中选择哪种方案？请通过计算说明．
相关试题
