【题目】如图,![]() ,
,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,
,
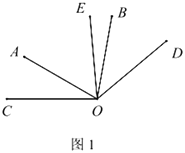
①若![]() ,则
,则![]() 的度数为______(直接写出结果);
的度数为______(直接写出结果);
②求![]() 的度数;
的度数;
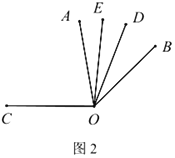
(2)将图1中的![]() 绕顶点
绕顶点![]() 顺时针旋转至图2的位置,试探究
顺时针旋转至图2的位置,试探究![]() 和
和![]() 的度数之间的关系,写出你的结论,并说明理由.
的度数之间的关系,写出你的结论,并说明理由.
参考答案:
【答案】(1)15°;(2)15°;(3)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)①由角的和差求出∠COD=140°,再根据角平分线的定义得出∠AOE=55°,最后根据∠AOE+∠BOE=70°求解即可;
②根据已知求出![]() ,再由角平分线的性质得出
,再由角平分线的性质得出![]() ,最后根据角的和差关系得出
,最后根据角的和差关系得出![]() ;
;
(2)设∠AOE=x,可得∠BOE=α-x,再由角的和差关系得出∠AOC=2(α-x),从而可以得出![]() .
.
(1)①∵α=70°,∠AOB=![]() ∠COD=α,
∠COD=α,
∴∠AOB=70°,∠COD=140°,
∵∠AOC=30°,
∴∠AOD=∠COD-∠AOC=140°-30°=110°,
∵OE平分∠AOD.
∴∠AOE=![]() ∠AOD=
∠AOD=![]() ×110°=55°,
×110°=55°,
∴∠BOE=∠AOB-∠AOE=70°-55°=15°,
故答案为:![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() 平分
平分![]() .
.
∴![]() ,
,
∴![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵![]() 平分
平分![]() ,
,
设![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)正方形ABCD,E、F分别在边BC、CD上(不与端点重合),∠EAF=45°,EF与AC交于点G
①如图(i),若AC平分∠EAF,直接写出线段EF,BE,DF之间等量关系;
②如图(ⅱ),若AC不平分∠EAF,①中线段EF,BE,DF之间等量关系还成立吗?若成立请证明;若不成立请说明理由
(2)如图(ⅲ),矩形ABCD,AB=4,AD=8.点M、N分别在边CD、BC上,AN=2
 ,∠MAN=45°,求AM的长度.
,∠MAN=45°,求AM的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过点D的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG,EF.

(1)说明:BG=CF;
(2)BE,CF与EF这三条线段能否组成一个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多0.5小时.设文艺小组每次活动时间为
 小时,请根据表中信息完成下列解答.
小时,请根据表中信息完成下列解答.课外小组活动
总时间(小时)
文艺小组
活动次数
科技小组
活动次数
七年级
12.5
4
3
八年级
10.5
3

九年级
7


(1)科技小组每次活动时间为______小时(用含
 的式子表示);
的式子表示);(2)求八年级科技小组活动次数
 的值;
的值;(3)直接写出
 ______,
______, ______.
______. -
科目: 来源: 题型:
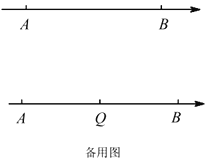
查看答案和解析>>【题目】如图,数轴上点
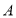 ,
,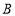 表示的数
表示的数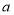 ,
,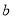 满足
满足 ,点
,点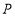 为线段
为线段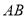 上一点(不与
上一点(不与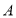 ,
,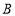 重合),
重合),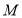 ,
,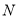 两点分别从
两点分别从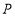 ,
,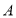 同时向数轴正方向移动,点
同时向数轴正方向移动,点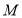 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点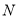 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为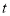 秒(
秒(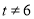 ).
).
(1)直接写出
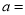 ______,
______,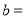 ______;
______;(2)若
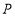 点表示的数是0.
点表示的数是0.①
 ,则
,则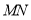 的长为______(直接写出结果);
的长为______(直接写出结果);②点
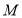 ,
,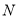 在移动过程中,线段
在移动过程中,线段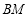 ,
, 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;(3)点
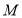 ,
,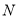 均在线段
均在线段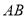 上移动,若
上移动,若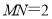 ,且
,且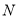 到线段
到线段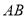 的中点
的中点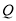 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点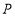 表示的数.
表示的数. -
科目: 来源: 题型:
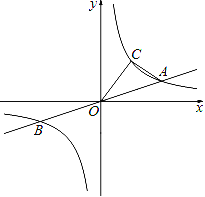
查看答案和解析>>【题目】已知:如图,直线y=
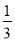 x与双曲线
x与双曲线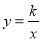 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).(1)求双曲线
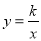 的解析式;
的解析式;(2)点C(n,4)在双曲线
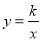 上,求△AOC的面积;
上,求△AOC的面积;(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
-
科目: 来源: 题型:
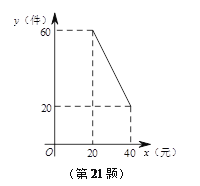
查看答案和解析>>【题目】某超市以20元/件的价格购进一批商品,根据前期销售情况,每天销售量y(件)与该商品的销售价x(元)之间的函数图象如图所示.
(1)求y与x之间的函数关系式.
(2)如果将该商品的销售价定为30元/件,不考虑其它因素,求该超市每天销售这种商品所能获得的利润.
(3)直接写出能使该超市获得最大利润的商品销售价
相关试题

