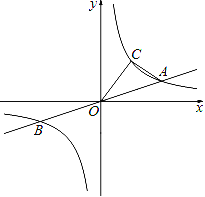
【题目】已知:如图,直线y=![]() x与双曲线
x与双曲线![]() 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).
(1)求双曲线![]() 的解析式;
的解析式;
(2)点C(n,4)在双曲线![]() 上,求△AOC的面积;
上,求△AOC的面积;
(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
参考答案:
【答案】(1)y=![]() ;(2)9;(3) P(3,0)或P(﹣3,0)
;(2)9;(3) P(3,0)或P(﹣3,0)
【解析】试题分析:(1)、首先根据一次函数的解析式得出点A的坐标,然后根据点A的坐标得出反比例函数的解析式;(2)、作CD⊥x轴于D点,AE⊥x轴于E点,根据题意得出点C的坐标,然后根据S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA得出答案;(3)、设P点坐标为(x,0)根据△AOP的面积求出x的值,从而得出点P的坐标.
试题解析:解:(1)∵点A(6,m)在直线y=![]() x上, ∴m=
x上, ∴m=![]() ×6=2,
×6=2,
∵点A(6,2)在双曲线![]() 上, ∴
上, ∴![]() ,解得k=12,
,解得k=12,
∴双曲线的解析式为y=![]() ;
;
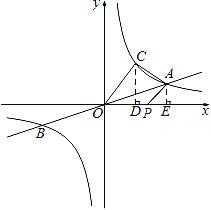
(2)作CD⊥x轴于D点,AE⊥x轴于E点,如图, ∵点C(n,4)在双曲线![]() 上,
上,
∴![]() ,解得n=3,即点C的坐标为(3,4), ∵点A,C都在双曲线
,解得n=3,即点C的坐标为(3,4), ∵点A,C都在双曲线![]() 上,
上,
∴S△OCD=S△AOE=![]() ×12=6, ∴S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA,
×12=6, ∴S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA,
∴S△AOC=![]() (CD+AE)DE=
(CD+AE)DE=![]() (4+2)×(6﹣3)=9;
(4+2)×(6﹣3)=9;
(3)∵S△AOC=9, ∴S△AOP=3,
设P点坐标为(x,0),而A点坐标为(6,2),
∴S△AOP=![]() ×2×|x|=3,解得x=±3,
×2×|x|=3,解得x=±3,
∴P(3,0)或P(﹣3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多0.5小时.设文艺小组每次活动时间为
 小时,请根据表中信息完成下列解答.
小时,请根据表中信息完成下列解答.课外小组活动
总时间(小时)
文艺小组
活动次数
科技小组
活动次数
七年级
12.5
4
3
八年级
10.5
3

九年级
7


(1)科技小组每次活动时间为______小时(用含
 的式子表示);
的式子表示);(2)求八年级科技小组活动次数
 的值;
的值;(3)直接写出
 ______,
______, ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
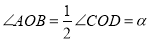 ,
,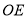 平分
平分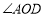 .
.(1)如图1,若
 ,
,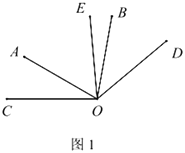
①若
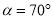 ,则
,则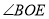 的度数为______(直接写出结果);
的度数为______(直接写出结果);②求
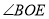 的度数;
的度数;(2)将图1中的
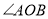 绕顶点
绕顶点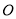 顺时针旋转至图2的位置,试探究
顺时针旋转至图2的位置,试探究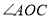 和
和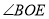 的度数之间的关系,写出你的结论,并说明理由.
的度数之间的关系,写出你的结论,并说明理由.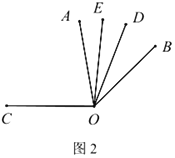
-
科目: 来源: 题型:
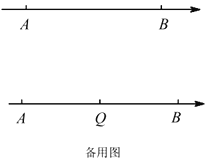
查看答案和解析>>【题目】如图,数轴上点
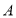 ,
,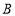 表示的数
表示的数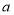 ,
,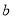 满足
满足 ,点
,点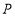 为线段
为线段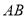 上一点(不与
上一点(不与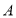 ,
,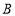 重合),
重合),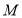 ,
,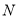 两点分别从
两点分别从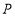 ,
,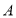 同时向数轴正方向移动,点
同时向数轴正方向移动,点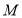 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点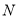 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为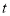 秒(
秒(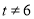 ).
).
(1)直接写出
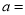 ______,
______,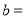 ______;
______;(2)若
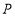 点表示的数是0.
点表示的数是0.①
 ,则
,则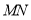 的长为______(直接写出结果);
的长为______(直接写出结果);②点
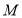 ,
,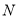 在移动过程中,线段
在移动过程中,线段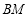 ,
, 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;(3)点
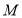 ,
,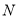 均在线段
均在线段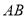 上移动,若
上移动,若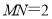 ,且
,且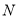 到线段
到线段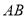 的中点
的中点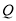 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点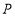 表示的数.
表示的数. -
科目: 来源: 题型:
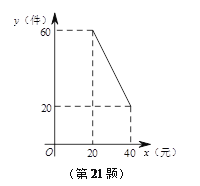
查看答案和解析>>【题目】某超市以20元/件的价格购进一批商品,根据前期销售情况,每天销售量y(件)与该商品的销售价x(元)之间的函数图象如图所示.
(1)求y与x之间的函数关系式.
(2)如果将该商品的销售价定为30元/件,不考虑其它因素,求该超市每天销售这种商品所能获得的利润.
(3)直接写出能使该超市获得最大利润的商品销售价
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
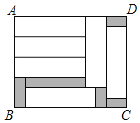
查看答案和解析>>【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形后,还有一部分空余(阴影部分),已知小长方形的长为a,宽为b,且a>b.
(1)用含a、b的代数式表示长方形ABCD的长AD和宽AB.
(2)用含a、b的代数式表示阴影部分的面积(列式表示即可,不要求化简).
(3)若a=7cm,b=2cm,求阴影部分的面积.
相关试题

