【题目】(1)正方形ABCD,E、F分别在边BC、CD上(不与端点重合),∠EAF=45°,EF与AC交于点G
①如图(i),若AC平分∠EAF,直接写出线段EF,BE,DF之间等量关系;
②如图(ⅱ),若AC不平分∠EAF,①中线段EF,BE,DF之间等量关系还成立吗?若成立请证明;若不成立请说明理由
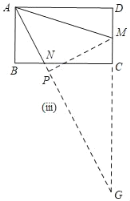
(2)如图(ⅲ),矩形ABCD,AB=4,AD=8.点M、N分别在边CD、BC上,AN=2![]() ,∠MAN=45°,求AM的长度.
,∠MAN=45°,求AM的长度.

参考答案:
【答案】(1)①EF=BE+DF;见解析;②,①中线段EF,BE,DF之间等量关系还成立:EF=BE+DF;见解析;(2)AM=![]() .
.
【解析】
(1)①结合题意由正方形ABCD的性质得到△ABE≌△ADF,则∠AGE=∠AGF=90°,又因为AE平分∠BAC,得到EF=BE+DF;
②作图延长CD到点H,截取DH=BE,连接AH,根据已知条件求证△AEB≌△AHD,则AE=AH,∠BAE=∠HAD,再证△EAF≌△HAF,则有EF=HF=DF+DH=BE+DF.
(2)根据矩形的性质,和相似△ABN∽△GCN,得到AP=PM,再设设AP=x,最终求得
AM.
(1)①如图(i),
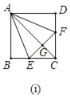
∵四边形ABCD是正方形,
∴∠BAC=∠CAD=45°,
∵∠EAF=45°,AC平分∠EAF,
∴∠BAE=∠EAG=∠DAF=∠FAG=22.5°,
∵AB=AD,∠B=∠D=90°,
∴△ABE≌△ADF(ASA),
∴BE=DF,AE=AF,
∴∠AEF=∠AFE,
∴AC⊥EF,
∴∠AGE=∠AGF=90°,
∵AE平分∠BAC,
∴BE=EG,DF=GF,
∴EF=BE+DF;
②,①中线段EF,BE,DF之间等量关系还成立:EF=BE+DF;
如图(ⅱ),延长CD到点H,截取DH=BE,连接AH,
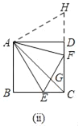
在△AEB与△AHD中,
∵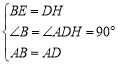 ,
,
∴△AEB≌△AHD(SAS),
∴AE=AH,∠BAE=∠HAD,
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAF+∠DAH=45°.即∠EAF=∠HAF,
在△EAF与△HAF中,
∵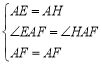 ,
,
∴△EAF≌△HAF(SAS),
∴EF=HF=DF+DH=BE+DF,
(2)如图(iii),延长AN,DC交于点G,过M作MP⊥AG于点P,
∵四边形ABCD是矩形,
∴∠B=90°,
Rt△ABN中,AB=4,AN=2![]() ,
,
∴BN=2,CN=8﹣2=6,
∵AB∥CG,
∴△ABN∽△GCN,
∴![]() ,
,
∴NG=6![]() ,
,
∵∠MAN=45°,∠APM=90°,
∴AP=PM,
设AP=x,则PM=2x,PG=2x,
∵AG=2![]() +6
+6![]() =x+2x,
=x+2x,
x=![]() ,
,
∴AM=![]() x=
x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC外作等腰三角形ABD和等腰三角形ACE,且∠BAD=∠CAE=90°,AM为△ABC中BC边上的中线,连接DE.求证:DE=2AM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,直线
 与
与 轴交于点
轴交于点 ,以
,以 为边长作等边
为边长作等边 ,过点
,过点 作
作 平行于
平行于 轴,交直线
轴,交直线 于点
于点 ,以
,以 为边长作等边
为边长作等边 ,过点
,过点 作
作 平行于
平行于 轴,交直线
轴,交直线 于点
于点 ,以
,以 为边长作等边
为边长作等边 ,…,则等边
,…,则等边 的边长是______.
的边长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过点D的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG,EF.

(1)说明:BG=CF;
(2)BE,CF与EF这三条线段能否组成一个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多0.5小时.设文艺小组每次活动时间为
 小时,请根据表中信息完成下列解答.
小时,请根据表中信息完成下列解答.课外小组活动
总时间(小时)
文艺小组
活动次数
科技小组
活动次数
七年级
12.5
4
3
八年级
10.5
3

九年级
7


(1)科技小组每次活动时间为______小时(用含
 的式子表示);
的式子表示);(2)求八年级科技小组活动次数
 的值;
的值;(3)直接写出
 ______,
______, ______.
______. -
科目: 来源: 题型:
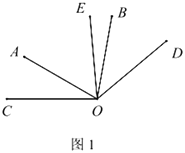
查看答案和解析>>【题目】如图,
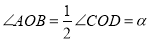 ,
,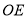 平分
平分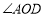 .
.(1)如图1,若
 ,
,
①若
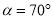 ,则
,则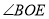 的度数为______(直接写出结果);
的度数为______(直接写出结果);②求
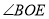 的度数;
的度数;(2)将图1中的
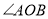 绕顶点
绕顶点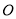 顺时针旋转至图2的位置,试探究
顺时针旋转至图2的位置,试探究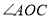 和
和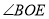 的度数之间的关系,写出你的结论,并说明理由.
的度数之间的关系,写出你的结论,并说明理由.
相关试题

