【题目】若存在正常数a,b,使得x∈R有f(x+a)≤f(x)+b恒成立,则称f(x)为“限增函数”.给出下列三个函数:①f(x)=x2+x+1;② ![]() ;③f(x)=sin(x2),其中是“限增函数”的是( )
;③f(x)=sin(x2),其中是“限增函数”的是( )
A.①②③
B.②③
C.①③
D.③
参考答案:
【答案】B
【解析】解:对于①,f(x+a)≤f(x)+b可化为:(x+a)2+(x+a)+1≤x2+x+1+b, 即2ax≤﹣a2﹣a+b,即x≤ ![]() 对一切x∈R均成立,
对一切x∈R均成立,
由函数的定义域为R,故不存在满足条件的正常数a、b,故f(x)=x2+x+1不是“限增函数”;
对于②,若f(x)= ![]() 是“限增函数”,则f(x+a)≤f(x)+b可化为:
是“限增函数”,则f(x+a)≤f(x)+b可化为: ![]() ≤
≤ ![]() +b,
+b,
∴|x+a|≤|x|+b2+2b ![]() 恒成立,又|x+a|≤|x|+a,∴|x|+a≤|x|+b2+2b
恒成立,又|x+a|≤|x|+a,∴|x|+a≤|x|+b2+2b ![]() ,∴
,∴ ![]() ≥
≥ ![]() ,
,
显然当a<b2时式子恒成立,∴f(x)= ![]() 是“限增函数”;
是“限增函数”;
对于③,∵﹣1≤f(x)=sin(x2)≤1,∴f(x+a)﹣f(x)≤2,
∴当b≥2时,a为任意正数,使f(x+a)≤f(x)+b恒成立,故f(x)=sin(x2)是“限增函数”.
故选B.
【考点精析】通过灵活运用全称命题,掌握全称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;全称命题的否定是特称命题即可以解答此题.
;全称命题的否定是特称命题即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为
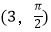 ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为  ,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )
A. 2 B. 3 C. 2或3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+a|+|x+
 |(a>0) (Ⅰ)当a=2时,求不等式f(x)>3的解集;
|(a>0) (Ⅰ)当a=2时,求不等式f(x)>3的解集;
(Ⅱ)证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若将f(x)的图象向左平移
,若将f(x)的图象向左平移  个单位后所得函数的图象关于原点对称,则φ=( )
个单位后所得函数的图象关于原点对称,则φ=( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足
内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足 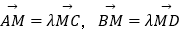 (其中λ>0,且λ≠1),若λ变化时,AB的斜率总为
(其中λ>0,且λ≠1),若λ变化时,AB的斜率总为  ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=5,在AC上取一E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )

A. 1 B.
 C. 2 D.
C. 2 D. 
相关试题

