【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.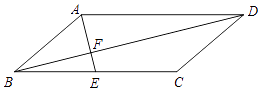
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
参考答案:
【答案】
(1)证明:∵四边形ABCD为平行四边形∴AD∥BC,AD=BC,AB=CD,
∵点E为BC的中点,
∴BE= ![]() BC=
BC= ![]() AD,
AD,
∵AD∥BC,
∴△BEF∽△DAF,
∴ ![]() =
= ![]() ,
,
∴DF=2BF
(2)解:∵CD= ![]() ,
,
∴AB=CD= ![]() ,
,
∵在Rt△ABF中,∠AFB=90°,∴tan∠ABD= ![]() =
= ![]() ,
,
∴设AF=x,则BF=2x,
∴AB= ![]() =
= ![]() x=
x= ![]() ,
,
∴x=1,AF=1,BF=2,
∵DF=2BF,
∴DF=4,
∴AD= ![]() =
= ![]()
【解析】(1)由平行四边形的性质的出AD∥BC,AD=BC,AB=CD,再据相似三角形的判定定理得△BEF∽△DAF,最后由相似三角形的对应边成比例得出DF=2BF;(2)由平行四边形的性质对边相等得出AB=CD,再Rt△ABF中由锐角三角函数,及勾股定理得出AD的长度。
【考点精析】利用平行四边形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划开发
 、
、 两种户型楼盘,设
两种户型楼盘,设 户型
户型 套,
套, 户型
户型 套,且两种户型的函数关系满足
套,且两种户型的函数关系满足 ,经市场调研,每套户型的成本价和预售价如下表所示:
,经市场调研,每套户型的成本价和预售价如下表所示:楼盘户型


成本价(万元/套)
60
80
预售价(万元/套)
80
120
若公司最多投入开发资金为14000万元,所获利润为
 万元,
万元,(1)求
 与
与 的函效关系式和自变量
的函效关系式和自变量 的取值范围
的取值范围(2)售完这批楼盘,公司所获得的最大利润是多少?
(3)公司在实际销售过程中,其他条件不变,
 户型每套销售价格提高
户型每套销售价格提高 (
( )万元,且限定
)万元,且限定 户型最多开发120套,则公司如何建房,利润最大?(注:利润=售价-成本.)
户型最多开发120套,则公司如何建房,利润最大?(注:利润=售价-成本.) -
科目: 来源: 题型:
查看答案和解析>>【题目】将一块直角三角板的直角顶点绕着矩形
 (
( )对角线交点
)对角线交点 旋转(如图①→②→③),
旋转(如图①→②→③), 、
、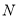 分别为直角三角板的直角边与矩形
分别为直角三角板的直角边与矩形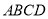 的边
的边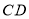 、
、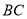 的交点.
的交点.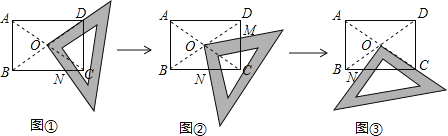
(1)发现:在图①中,当三角板的一直角边与
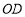 重合,易证
重合,易证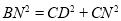 ,
,证明方法如下:连接
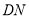 ,
,∵
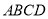 为矩形
为矩形∴
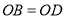
又∵
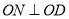
∴
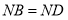
又∵
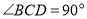
∴
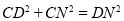
∴
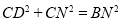
在图③中,当三角板的一直角边与
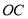 重合,求证:
重合,求证: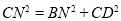 .
.(2)根据以上学习探究:图②中
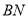 、
、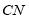 、
、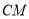 、
、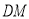 这四条线段之间的数量关系,写出你的结论,并说明理由.
这四条线段之间的数量关系,写出你的结论,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.
求证:BE=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①
 ;②
;② ;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定.由统计图可知正确的结论是( )
;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定.由统计图可知正确的结论是( )
A. ①③B. ①④C. ②③D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm.
(1)写出y与x之间的关系式;
(2)当该动物腿长10dm时,其身高为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数
100
200
300
500
800
1000
3000
摸到白球的次数
65
124
178
302
480
601
1800
摸到白球的频率







(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?
相关试题

