搜索
【题目】如图，在等边△ABC中，点D为边BC的中点，以AD为边作等边△ADE，连接BE．
求证：BE=BD．
参考答案：
【答案】证明：∵在等边△ABC中，点D为边BC的中点，
∴∠CAD=∠DAB= 
∠CAB=30°，
∵△ADE为等边三角形，
∴AD=AE，∠DAE=60°，
∵∠DAB=30°，
∴∠DAB=∠EAB=30°，
在△ADB与△AEB中，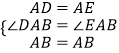 
，
∴△ADB≌△AEB（SAS），
∴BE=BD．
【解析】由等角三角形的三线合一得出∠CAD=∠DAB=30°，再由等边三角形的性质得出AD=AE，∠DAE=60°，进而判断出△ADB≌△AEB，再由三角形全等对应边相等得出结论。
【考点精析】通过灵活运用等边三角形的性质，掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有大小两种货车，3辆大货车与4辆小货车一次可以运货27吨，2辆大货车与6辆小货车一次可以运货28吨．
（1）请问1辆大货车和1辆小货车一次可以分别运货多少吨；
（2）目前有45吨货物需要运输，货运公司拟安排大小货车共计10辆，全部货物一次运完，其中每辆大货车一次运货费用150元，每辆小货车一次运货费用100元，请问货运公司应如何安排车辆最节省费用？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司计划开发
、
两种户型楼盘，设户型
套，户型
套，且两种户型的函数关系满足
，经市场调研，每套户型的成本价和预售价如下表所示：楼盘户型
成本价（万元/套）
60
80
预售价（万元/套）
80
120
若公司最多投入开发资金为14000万元，所获利润为
万元，（1）求
与的函效关系式和自变量的取值范围（2）售完这批楼盘，公司所获得的最大利润是多少？
（3）公司在实际销售过程中，其他条件不变，
户型每套销售价格提高
（
）万元，且限定户型最多开发120套，则公司如何建房，利润最大？（注：利润=售价－成本．） -
科目： 来源： 题型：
查看答案和解析>>【题目】将一块直角三角板的直角顶点绕着矩形
（
）对角线交点
旋转（如图①→②→③），
、
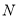分别为直角三角板的直角边与矩形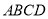的边
、
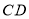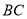的交点．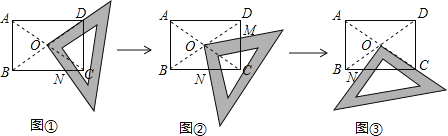
（1）发现：在图①中，当三角板的一直角边与
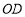重合，易证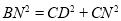
，证明方法如下：连接
，∵
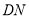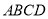为矩形∴
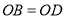
又∵
∴
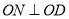
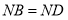
又∵
∴
∴
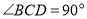
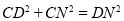
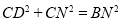
在图③中，当三角板的一直角边与
重合，求证：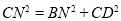
．（2）根据以上学习探究：图②中
、
、
、
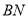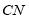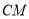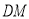这四条线段之间的数量关系，写出你的结论，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，点E为BC的中点，AE与对角线BD交于点F．
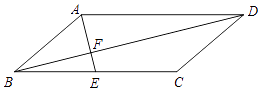
（1）求证：DF=2BF；
（2）当∠AFB=90°且tan∠ABD=
时，若CD=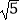 
，求AD长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①
；②
；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定．由统计图可知正确的结论是（ ）
A. ①③B. ①④C. ②③D. ②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种动物的身高y（dm）是其腿长x（dm）的一次函数．当动物的腿长为6dm时，身高为45.5dm；当动物的腿长为14dm时，身高为105.5dm．
（1）写出y与x之间的关系式；
（2）当该动物腿长10dm时，其身高为多少？
相关试题
