【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线![]() ,点D在点C的左边。
,点D在点C的左边。
(1)若BD平分∠ABC,![]() ,则
,则![]() _____°;
_____°;
(2)如图②,若![]() ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明![]() ;
;
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中![]() 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.

参考答案:
【答案】(1)10;(2)证明见解析;(3)不变,![]()
【解析】
(1)根据两直线平行,内错角相等得∠ABD=![]() ,由BD平分∠ABC得∠ABC=2∠ABD=80°,根据垂直即可得∠OCB的度数;
,由BD平分∠ABC得∠ABC=2∠ABD=80°,根据垂直即可得∠OCB的度数;
(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠CFE;
(3)由∠ABC+∠ACB=2∠DAC,∠H+∠HCA=∠DAC,∠ACB=2∠HCA,求出∠ABC=2∠H,即可得答案.
解:(1)∵直线![]() ,
,![]() ,
,
∴∠ABD=![]() ,
,
∵BD平分∠ABC,
∴∠ABC=2∠ABD=80°,
又∵直线MN⊥直线PQ,
∴∠OCB=90°-∠ABC=10°;
(2)∵![]() ,∴
,∴![]()
∴![]()
∵直线![]() 直线PQ
直线PQ
∴![]()
∵![]()
∴![]()
∵BF是∠CBA的平分线,
∴![]()
∴![]() ;
;
(3)不变
∵直线![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵CH是∠ACB的平分线
∴![]()
∴![]()
∴![]() .
.
故答案为:(1)10;(2)证明见解析;(3)不变,![]() .
.
-
科目: 来源: 题型:
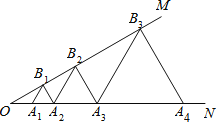
查看答案和解析>>【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.
-
科目: 来源: 题型:
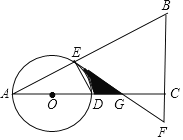
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次
第2次
第3次
提现金额(元)
A
b

手续费(元)
0
0.4
3.4
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一块在电脑屏幕上出现的长方形色块图,由6个不同的正方形组成。设中间最小的一个正方形边长为1,则这个长方形色块图的面积为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长度;
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜测出MN的长度吗?请说出你发现的结论,并说明理由.
-
科目: 来源: 题型:
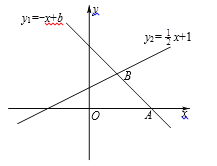
查看答案和解析>>【题目】如图,已知一次函数y1=-x+b的图象交x轴于点A(3,0),与一次函数y2=
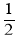 x+1的图象交于点B,
x+1的图象交于点B,(1)求一次函数y1=-x+b的表达式;
(2)当x取哪些值时,0<y1<y2?
相关试题

