搜索
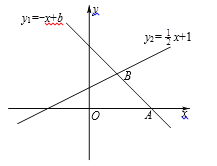
【题目】如图，已知一次函数y1=-x+b的图象交x轴于点A（3，0），与一次函数y2=
x+1的图象交于点B,
（1）求一次函数y1=-x+b的表达式；
（2）当x取哪些值时，0<y1<y2？
参考答案：
【答案】（1）y1=-x+3；（2）
【解析】
(1)由一次函数y1=-x+b的图象交x轴于点A（3，0），用待定系数法列式求解即可得到答案；
(1)先求出两个一次函数函数的交点坐标，观察图像可以直接得到答案；
解：（1）∵一次函数y1=-x+b的图象交x轴于点A（3，0），
将点A（3，0）代入y1=-x+b，
得0=-3+b，解得b=3，
所以一次函数y1=-x+b的表达式为y1=-x+3；
（2）当-x+3=
x+1时，
解得：
，即点B的横坐标为
，
观察图象可知，
当时，0<y1<y2；
-
科目： 来源： 题型：
查看答案和解析>>【题目】己知：如图①，直线MN⊥直线PQ，垂足为O，点A在射线OP上，点B在射线OQ上（A、B不与O点重合），点C在射线ON上，过点C作直线
，点D在点C的左边。（1）若BD平分∠ABC，
，则
_____°；（2）如图②，若
，作∠CBA的平分线交OC于E，交AC于F，试说明
；（3）如图③，若∠ADC=∠DAC，点B在射线OQ上运动，∠ACB的平分线交DA的延长线于点H.在点B运动过程中
的值是否变化？若不变，求出其值；若变化，求出变化范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是一块在电脑屏幕上出现的长方形色块图，由6个不同的正方形组成。设中间最小的一个正方形边长为1，则这个长方形色块图的面积为_____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，点C在线段AB上，且AC=6cm，BC=14cm，点M、N分别是AC、BC的中点．
（1）求线段MN的长度；
（2）在（1）中，如果AC=acm，BC=bcm，其它条件不变，你能猜测出MN的长度吗？请说出你发现的结论，并说明理由．
-
科目： 来源： 题型：
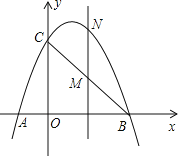
查看答案和解析>>【题目】如图，已知抛物线经过点A(－1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N若点M的横坐标为m，请用m的代数式表示MN的长。
(3)在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】公园里有一人设了个游戏摊位，游客只需掷一枚正方体骰子，如果出现3点，就可获得价值10元的奖品，每抛掷1次骰子只需付1元的费用．小明在摊位前观察了很久，记下了游客的中奖情况：
游客
1
2
3
4
5
6
7
抛掷次数
30
20
25
6
16
50
12
中奖次数
1
0
0
1
0
2
0
看了小明的记录，你有什么看法？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为
．（1）试求袋中绿球的个数；
（2）第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率．
相关试题
