【题目】如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求![]() 的度数;
的度数;
(2)若BC=9,AC=12,求BD的长.

参考答案:
【答案】(1)![]() 的度数是50°;(2) BD=
的度数是50°;(2) BD=![]() .
.
【解析】
(1)求出∠B的度数,求出∠B所对的弧的度数,即可得出答案;
(2)根据勾股定理求出AB,根据割线定理得出比例式,即可得出答案.
(1)延长BC交☉O于点N,
∵在△ABC中,∠C=90°,∠A=25°,∴∠B=65°,
∴∠B所对的弧BDN的度数是130°,
∴![]() 的度数是180°-130°=50°.
的度数是180°-130°=50°.
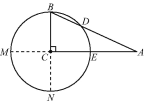
(2)延长AC交☉O于点M,
在Rt△BCA中,由勾股定理得AB=![]() =15,
=15,
∵BC=9,AC=12,
∴CM=CE=BC=9,AM=AC+CM=21,AE=AC-CE=3,
由割线定理得AD×AB=AE×AM,
∴(15-BD)×15=21×3,解得BD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是边长为1的正方形,
是边长为1的正方形, 与
与 轴正半轴的夹角为15°,点
轴正半轴的夹角为15°,点 在抛物线
在抛物线 的图象上,则
的图象上,则 的值为( )
的值为( )
A.
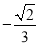 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能写成
 的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。(1)请证明:28和217都是婆罗摩笈多数。
(2)请证明:任何两个婆罗摩笈多数的乘积依旧是婆罗摩笈多数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ED为☉O的直径且ED=4,点A(不与点E,D重合)为☉O上一个动点,线段AB经过点E,且EA=EB,F为☉O上一点,∠FEB=90°,BF的延长线交AD的延长线于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在☉O上移动时,直接回答四边形FCDE的最大面积为多少.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下述材料:
下述形式的繁分数叫做有限连分数,其中n是自然数,a0是整数,a1,a2,a3,…,an是正整数:

其中
 称为部分商。
称为部分商。按照以下方式可将任何一个分数转化为连分数的形式:
 ,则
,则 ;考虑
;考虑 的倒数,有
的倒数,有 ,从而
,从而 ;再考虑
;再考虑 的倒数,有
的倒数,有 ,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
可利用连分数来求二元一次不定方程的特殊解,以
 为例,首先将
为例,首先将 写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数
写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数 ,从而
,从而 是一个特解。
是一个特解。考虑不定方程
 ,先将
,先将 写成连分数的形式:
写成连分数的形式: 。
。注意到此连分数有奇数个部分商,将之改写为偶数个部分商的形式:

计算倒数第二个渐近分数:
 ,所以
,所以 是
是 的一个特解。
的一个特解。对于分式,有类似的连分式的概念,利用将分数展开为连分数的方法,可以将分式展开为连分式。例如
 的连分式展开式如下,它有3个部分商:
的连分式展开式如下,它有3个部分商:
 ;
;
再例如,
 ,它有4个部分商:1,
,它有4个部分商:1, 。
。请阅读上述材料,利用所讲述的方法,解决下述两个问题
(1)找出两个关于x的多项式p和q,使得
 。
。(2)找出两个关于x的多项式u和v,使得
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
相关试题

