【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当 ![]() ≤S 四边形≤
≤S 四边形≤![]() 时,求BD的取值范围;
时,求BD的取值范围;
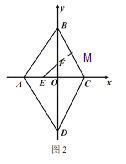
(3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①![]() ;②
;② ![]() ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
参考答案:
【答案】(1)①菱形和正方形;②![]() ab;(2)
ab;(2)![]() ≤BD≤2;(3)点P走完全程所需的时间t=
≤BD≤2;(3)点P走完全程所需的时间t=![]() ,直线EF的解析式为y=
,直线EF的解析式为y=![]() x+
x+![]() .
.
【解析】
(1)①根据菱形,正方形和矩形的性质即可判断;
②根据对角线互相垂直的四边形的面积等于对角线乘积的一半计算即可;
(2)设AC的长为x,根据△ABC为等腰直角三角形,△ACD为等边三角形,得出OB=![]() x,OD=
x,OD=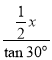 =
=![]() x,即BD=
x,即BD=![]() x+
x+![]() x,再根据
x,再根据![]() ≤S四边形≤
≤S四边形≤![]() 运算即可;
运算即可;
(3)首先设A(-a,0),B(0,b),C(c,0),D(0,-d),然后根据![]() ,
,![]() ,得出a=c,b=d,再结合已知条件推吹四边形ABCD是有一个角为60°的菱形,根据菱形ABCD的周长为32,即可得出AB=8,OA=4,OB=
,得出a=c,b=d,再结合已知条件推吹四边形ABCD是有一个角为60°的菱形,根据菱形ABCD的周长为32,即可得出AB=8,OA=4,OB=![]() ,OE=2,过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=
,OE=2,过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=![]() FB,可得点P的运动时间t=
FB,可得点P的运动时间t=![]() =EF+
=EF+![]() FB=EF+FM,当E,F,M三点共线时EF+FM的值最小,由此可推出t=
FB=EF+FM,当E,F,M三点共线时EF+FM的值最小,由此可推出t=![]() ;根据在Rt△EOF中,OE=2,∠FEO=30°,可推出F(0,
;根据在Rt△EOF中,OE=2,∠FEO=30°,可推出F(0,![]() ),再结合点E的坐标为(-2,0),即可求出EF的解析式.
),再结合点E的坐标为(-2,0),即可求出EF的解析式.
(1)①∵菱形和正方形的对角线互相垂直,矩形的对角线不互相垂直,
∴菱形和正方形一定是十字形;
②对角线互相垂直的四边形的面积等于对角线乘积的一半,
∴四边形的面积为![]() ab;
ab;
(2)设AC的长为x,
∵△ABC为等腰直角三角形,△ACD为等边三角形,
∴OB=![]() x,OD=
x,OD=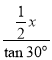 =
=![]() x,
x,
∴BD=![]() x+
x+![]() x,
x,
∵![]() ≤S四边形≤
≤S四边形≤![]()
![]() ≤
≤![]() x(
x(![]() x+
x+![]() x)≤
x)≤![]()
![]() ≤
≤![]() x2≤
x2≤![]()
![]() ≤x2≤
≤x2≤![]()
![]() ≤x≤
≤x≤![]()
∴![]() ≤
≤![]() x≤
x≤![]()
即![]() ≤BD≤2;
≤BD≤2;
(3)设A(-a,0),B(0,b),C(c,0),D(0,-d),
∴S1=![]() ab,S2=
ab,S2=![]() cd,S3=
cd,S3=![]() ad,S4=
ad,S4=![]() bc,
bc,
∵![]() ,
,![]() ,
,
∴S=S1+S2+![]() =
=![]() ab+
ab+![]() cd+
cd+![]() ,
,
S=S3+S4+![]() =
=![]() ad+
ad+![]() bc+
bc+![]() ,
,
即![]() ab+
ab+![]() cd=
cd=![]() ad+
ad+![]() bc
bc
![]() ab-
ab-![]() ad=
ad=![]() bc-
bc-![]() cd
cd
![]() a(b-d)=
a(b-d)=![]() c(b-d)
c(b-d)
即a=c,同理b=d,
∴△AOB≌△BOC,△AOB≌△AOD,
∴AB=BC,AB=AD,
∵∠ABC=60°,
∴四边形ABCD是有一个角为60°的菱形,
∵菱形ABCD的周长为32,
∴AB=8,OA=4,OB=![]() ,
,
∵点E为OA的中点,
∴OE=2,
过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=![]() FB,
FB,
∴点P的运动时间t=![]() =EF+
=EF+![]() FB=EF+FM,
FB=EF+FM,
∴当E,F,M三点共线时EF+FM的值最小,
∵∠ECM=60°,AC=AB,点E为OA的中点,
∴CE=6,∠∠FEO=30°,E(-2,0),
∴CM=3,EM=![]() ,即t=
,即t=![]() ,
,
在Rt△EOF中,OE=2,∠FEO=30°,
∴OF=![]() ,即F(0,
,即F(0,![]() ),
),
∴设EF的解析式为y=kx+b,
将E,F的坐标代入得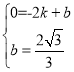 ,
,
解得: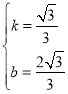 ,
,
∴EF的解析式为y=![]() x+
x+![]() ,
,
综上:点P走完全程所需的时间t=![]() ,直线EF的解析式为y=
,直线EF的解析式为y=![]() x+
x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的三个顶点A,O,C在坐标轴上,矩形的面积为12,对角线AC所在直线的解析式为y=kx-4k(k≠0).
(1)求A,C的坐标;
(2)若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;
(3)在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB//EF,∠2=2∠1

(1)证明∠FEC=∠FCE;
(2)如图2,M为AC上一点,N为FE延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM有何数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表 100m 长.已知 各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).

(1)请写出图中下列地点的坐标:
牡丹园 ; 游乐园 ;
(2)连接音乐台、湖心亭和望春亭这三个 地点,画出所得的三角形.然后将所 得三角形向下平移 200m,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对应点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

相关试题

