【题目】如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表 100m 长.已知 各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).

(1)请写出图中下列地点的坐标:
牡丹园 ; 游乐园 ;
(2)连接音乐台、湖心亭和望春亭这三个 地点,画出所得的三角形.然后将所 得三角形向下平移 200m,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对应点的坐标为 .
参考答案:
【答案】(1)(300,300),(200,200);(2)见解析;(3)(300,0).
【解析】
(1)根据已知中心广场为原点,进而得出各点坐标即可;
(2)利用平移的性质进而得出平移后三角形即可;
(3)利用所画图形进而得出湖心亭平移后的对应点的坐标.
(1)∵东门的坐标为(400,0),
∴牡丹园坐标为:(300,300),游乐园坐标为:(200,200);
故答案为:(300,300),(200,200);
(2)如图所示:△ABC即为所求;
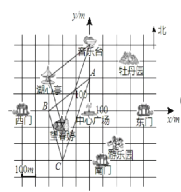
(3)湖心亭平移后的对应点的坐标为:(300,0).
故答案为:(300,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB//EF,∠2=2∠1

(1)证明∠FEC=∠FCE;
(2)如图2,M为AC上一点,N为FE延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM有何数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当
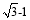 ≤S 四边形≤
≤S 四边形≤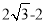 时,求BD的取值范围;
时,求BD的取值范围; (3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①
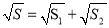 ;②
;② 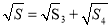 ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.
 B.4C.2D.无法确定
B.4C.2D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=
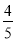 ,求BF的长.
,求BF的长.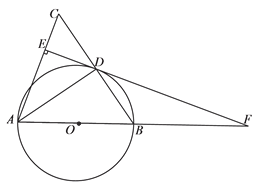
相关试题

